В равнобедренной трапеции углы при основаниях равны => ∠A = ∠D, ∠B = ∠C.
Проведем перпендикуляры из вершин B и C к стороне AD в точки K и L соответственно.
Получился прямоугольник KBCL (BC || AD, по свойству трапеции, BK ⊥ AD и CL ⊥ AD, BK || CL, все углы прямые). В прямоугольнике противоположные стороны равны, BC = KL = 12см.
AD = AK + KL + LD.
Рассмотрим треугольник ABK, лн прямоугольный, ∠AKB = 90°, ∠BAK = 30°, AB = 5см (гипотенуза, лежит против угла 90°).
По свойству прямоугольного треугольника: катет, лежащий против угла в 30°, равен половине гипотенузы. =>
BK = 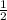 AB =
AB =  см =
см = 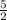 см.
см.
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. =>
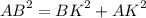
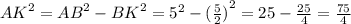 ,
,
AK = 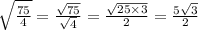 см.
см.
Треугольники ABK и LCD равны.
По трём углам:
∠BAK = ∠LDC = 30°,
∠AKB = ∠CLD = 90°,
∠ABK = ∠LCD = 180° – 30° – 90° = 60°.
Или по двум сторонам и углу между ними:
AB = CD = 5см,
BK = CL — противоположные стороны прямоугольника,
∠ABK = ∠LCD = 60°.
Также по стороне и прилегающим к ней двум углам.
По всем трём признакам равенства треугольников, треугольники равны (можно выбрать один из признаков).
=> AK = LD = 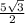 см.
см.
AD = AK + KL + LD = 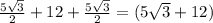 см.
см.
ответ: 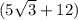 см
см


S = 50 ед².
Объяснение:
Пусть стороны прямоугольного параллелепипеда, образующие его измерения, равны "a", "b" и "c". Тогда площади основания и двух боковых граней равны
a·b = 48 (1), a·c = 40 (2) и b·c = 30 (3).
Выразим сторону b из равенств (1) и (3) и приравняем полученное:
b = 48/a и b = 30/c => 48/a = 30/c => c = 30a/48 = (5/8)a.
Подставим это значение в (2):
a·(5/8)a = 40 => a² = 320/5 = 64 => a = 8 ед.
Тогда из (1) b = 48/8 = 6 ед. c = 30/8 = 5 ед. (из 2).
Найдем по Пифагору диагональ основания:
d = √(a²+b²) = √(64+36) = 10 ед.
Площадь диагонального сечения равна:
S = d·c = 10·5 = 50 ед².