ответ: 16 (ед. объёма)
Подробное объяснение:
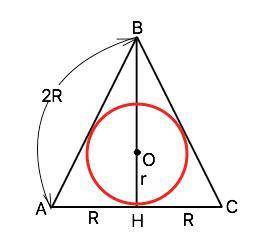
Схематический рисунок осевого сечения шара, вписанного в конус – окружность с радиусом r (радиус шара), вписанная в треугольник АВС. В данной задаче треугольник АВС правильный, его сторона равна диаметру основания конуса. ⇒ АВ=ВС=АС=d=2R
Высота ВН треугольника АВС – высота конуса ВН=АВ•sin60°=2R•√3/2=R√3. Подставим значение высоты в формулу объёма конуса:
V(к)=πR²•h/3= πR²•R√3/3=πR³/√3 ⇒ πR³/√3=36
Радиус r окружности, вписанной в правильный треугольник, равен 1/3 высоты этого треугольника ( высоты конуса). r=OH=(R√3):3=R/√3
Подставим найденное значение радиуса шара в формулу его объёма:
V(ш)=4π(R/√3)³/3=4πR³/9√3
Из найденного объёма конуса πR³/√3=36
подставим это значение в выражение объёма шара:
V(ш)=4•36/9=16 (ед. объёма)
сделать что-то простое :)
Чтобы найти высоту, надо сначала найти площадь. А чтобы найти площадь, надо найти размеры сторон - и диагоналей тоже.
Ромб делится диагоналями на четыре равных прямоугольных треугольника. У каждого из них катеты - это половинки диагоналей, а гипотенуза равна боковой стороне. Боковая сторона задана - это 200/4 = 50.
Далее речь идет об этом прямоугольном треугольнике.
Поскольку катеты отностятся как 3:4, то это "египетский" треугольник, то есть треугольник, подобный треугольнику со стронами 3,4,5. Поскольку гипотенуза равна 50, катеты равны 30 и 40.
Технически это можно проделать и "тупым" и не одним :) - можно например так.
Пусть один катет 3*х тогда другой 4*х, тогда
3^2*x^2 + 4^2*x^2 = 50^2;
x^2 = 100; x = 10; катеты 30 и 40.
Площадь такого треугольника 30*40/2 = 600;
Площадь всего ромба в 4 раза больше, то есть 2400;
Площадь равна высоте, умноженной на боковую сторону, то есть высота равна
2400/50 = 48.
Такой вот неприятный случай, простое и очевидное замечание вызвало, мягко говоря, сильное непонимание. Придется кое что объяснить.
Если очень трудно сосчитать площадь АВС (обозначения на рисунке sana2008), как АС*ВО/2 = 60*40/2 = 1200, или на тот случай, когда трудно сосчитать площадь ромба как АС*BD/2 = 2400, то
в этом случае, конечно, надо применить формулу Герона, она очень кстати.
Применяем её для треугольника АВС. АВ =ВС = 50, АС = 60, p = (50+50+60)/2 = 80;
р - ВС = р - АВ = 30
р - АС = 20
S^2 = 80*30*30*20 = (1200)^2
S = 1200
Ну и конечно - графически. Только вот сколько не строй "египетский" треугольник с гипотенузой 50, у него высота все равно 24. А это как раз расстояние от центра ромба до стороны, высота ромба в 2 раза больше.
Ошибка у sana2008 тривиальная, она почему то использовала АС = 30 и получила неверный результат, хотя отлично знала что АС = 60. Это бывает... но зачем же упрямиться :
ответ:пирамиды равен 3072 см3, сторона основания пирамиды a=24 см.
Объяснение: