Если в трапеции провести среднюю линюю, то она будет параллельна основаниям. Теперь рассмотрим треугольник, образованный диагональю, боковой стороной и МЕНЬШИМ основанием. В этом треугольнике часть средней линии трапеции тоже будет средней линией (параллельна основанию и проходит через середину одной стороны), поэтому средняя линяя трапеции проходит через середину диагонали. Кроме того, отрезок средней линии трапеции между диагональю и боковой стороной равен половине МЕНЬШЕГО основания.
Ясно, что все это справедливо и для другой диагонали, другой боковой стороны и другого отрезка средней линии между ними.
Получилось, средняя линяя проходит через середины диагоналей, и делится диагоналями на три отрезка, крайние из который равны половине меньшего основания.
Третий отрезок (a и b - основания трапеции, b - меньшее)
x = (a + b)/2 - (b/2 + b/2) = (a - b)/2, чтд.
На самом деле про середины можно сразу сослаться на теорему о пропорциональных отрезках секущих линий между параллельными прямыми. Из неё сразу следует, что прямая, проходящая через середину какой-то боковой стороны, поделит пополам и диагонали, и другую боковую сторону, и высоту, и вообще любой прямой отрезок, соединяющий точки верхнего и нижнего оснований.
Что касается расчета, то и его можно сделать проще, хотя казалось бы - куда проще.
Дело в том, что отрезок средней линии от левой боковой стороны до ближайшей диагонали равен половине меньшего основания (как средняя линия в треугольнике, образованном левой боковой стороной, меньшим основанием и этой диагональю), а - ТОЧНО ТАК ЖЕ - отрезок средней линии трапеции от левой боковой стороны до СЛЕДУЮЩЕЙ диагонали является средней линией в треугольнике, образованном левой боковой стороной, большим основанием и этой самой диагональю, то есть это отрезок равен половине большего основания. Искомый же отрезок равен их разности, откуда сразу получается ответ, даже и считать ничего не надо.
Дано: 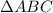
AB = BC = AC
AK - медиана
ВК = СК = 8дм
__________________
Найти AB, AC, BC.
1) Раз ВК и СК 8дм, значит по теореме о сумме отрезков ВС = ВК + СК = 8дм + 8дм = 16 дм
2) Раз АС = ВС = АВ (по условию), а ВС = 16дм (по 1 пункту моего решения), то АС = АВ = ВС = 16 дм.
ответ: АС = ВС = АВ = 16дм.
Углы рівнобічної трапеции относятся как 1:3, меньшая основа равна 2, а высота трапеции 4. найти площадь
Объяснение:
АВСМ-трапеция , АВ=СМ, ВС=2, ∠А:∠В=1:3, ВК⊥АМ, ВМ=4. Найти S.
Пусть одна часть равна х, тогда ∠А=1х ,∠В=3х. Углы ∠А и ∠В по расположени. односторонние ( АМ║ВС, АВ-секущая), значит ∠А+∠В=180° или 1х+3х=180° или х=45°.Значит∠А=45°.
ΔАВК-прямоугольный и равнобедренный , т.к. ∠АВК=90°-45°=45°⇒ высота ВК=АК=8 .
Проведем вторую высоту СР⊥АМ, тогда КР=ВС=2 , и РМ=АК , т.к трапеция равнобедренная. Значит АМ=4+2+4=10.
S( тр) =1/2*h*(а+в) , S( тр) =1/2*4*(10+2)=24 (ед²) .