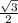и он равен отношению длины не найденной стороны к гипотенузе. Получается, что другая сторона равна произведению синуса угла в 60 градусов на гипотенузу, то есть диагональ, подставляя, получаем, что сторона равна 
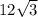. Площадь - произведение сторон. 12*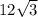=144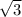
.
Угол АОВ и ДОС вертикальны, а в прямоугольнике вертикальные углы равны, а значит угол АОД= ВОС. Угол АОВ и угол ВОС- смежные, а значит, чтосумма смежных углов равна 180 градуса, то мы можем найти острый угол ВОС, а именно 180-92=88 градуса. Наш ответ 88