Полезно помнить, что высота тупоугольного треугольника, проведенная из вершины острого угла, расположена ВНЕ треугольника и пересекает продолжение стороны. к которой проведена.
* * *
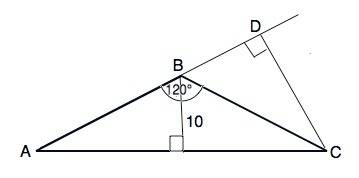
В равнобедренном треугольнике с углом при вершине, равным 120°, углы при основании равны (180°-120°):2=30°
Обозначим высоту, проведенную к основанию, ВН. По условию ВН=10.
В прямоугольном ∆ АВН гипотенуза АВ=ВН:sin30°=20
В прямоугольном ∆ ВDС угол CBD=60° (смежный углу АВС). ⇒
угол ВСD=30°,
В ∆ АВС стороны ВС=АВ=20 см, ⇒ BD=BC•sin30°=20•0,5=10 см
AD=AB+DB=20+10=30 см
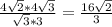см³≈7,54 см³
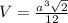где а - длина его ребра.
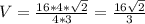см³
Боковая сторона равнобедренного треугольника равна 13см, а
основа – 10см. Найдите высоту, проведенную к основанию данного
треугольника.
Объяснение:
Δ АВС, АВ=ВС=13 см, АС=10 см, ВН-высота. ВН-?
Высота в равнобедренном треугольнике является медианой, значит АН=НС=5 см.
ΔАВН-прямоугольный, по т. Пифагора АВ²=АН²+ВН² ,
169=25+ВН² , ВН²=144 , ВН=12 см