56°
Объяснение:
мы разделяем окружность на несколько частей и затем находим углы как вписанные и центральные
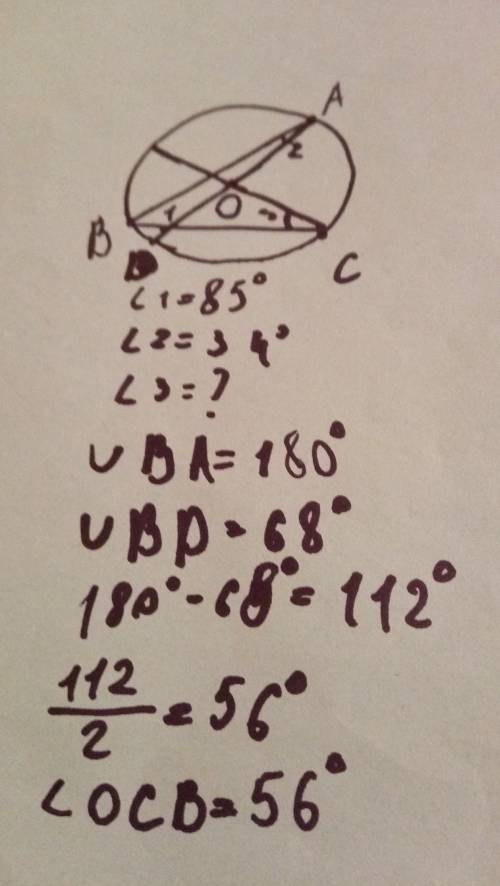
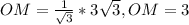
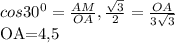
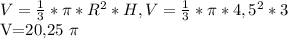
Если сторон и два прилежащих к ней угла одного треугольника соответственно равны двум углам прилежащих к ней другого треугольника, то такие треугольники равны
Объяснение:
Дано: треугольник АВС и А1В1С1. АС=А1С14 угол А= углу А1; угол С= углу С1.
Доказать: что треугольники равны
Док-во:
1.Наложим треугольник А1В1С1 на треугольники АВС, так чтобы АС совпало с А1С1
2. Т.к угол А= углу А1, луч А1В1 сонаправлен с лучом АВ
угол с= углу С1, луч С1В1 сонаправлен с лучом СВ
Из этого всего следует, что точки в и В1 совпадут.
3. Треугольник АВС и треугольник А1В1С1 совпали => треуг. АВС= треуг. А1В1С1
Точка 0 — центр окружности, на которой лежат точки А, В и С. Известно, что ABC = 85° и ОАВ = 34°. Найдите
угол ВCO. ответ дайте в градусах.