Гипотенуза = √52 = 2√13 см
Объяснение:
По теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы (c² = a² + b², где с - гипотенуза, а a и b - катеты).
Нам даны длины катетов, можем найти гипотенузу:
c² = 4² + 6² = 16 + 36 = 52 см
c = √52 = 2√13 см
S полной поверхности параллелепипеда = 2 S основания + 4 S боковой грани
S основания = S ромба =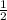
* на произведение диагоналей, одна диагональ = стороне. образовывает треугольник с углами 60 град. (формула для решения)
это равносторонний треугольник
2 диагональ из равностороннего треугольника со стороной a, и высотой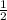 a и углом в вершине 120 град. В нем: прямоугольный треугольник с сторонами 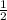*a (половина 1 диагонали), гипотенуза = a.
По т.пифагора: (корень из 3)*a/2
2 диагональ (равна корень из 3)*a
площадь основания = (корень из 3)*a*a/2.
найдем высоту. 45 град. угол между диагональю параллелепипеда и 2 диагональю ромба.
в треугольнике, образованном диагональю параллелепипеда диагональю ромба и боковой стороной параллелепипед один угол 45 град, второй = 90 град, то третий будет 180 - 45 - 90.
данный треугольник - равносторонний и высота равна диагонали ромба т.е. (корень из 3)*a. (в следствии)
Следовательно площадь боковой грани = a*(корень из 3)*a
Итого П.П.П. = 2*(корень из 3)*a*a/2 + 4*a*(корень из 3)*a = 5*(корень из 3)*(a в квадрате) (формулой)
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.
Объяснение:
Рисунок прилагается.
Дано: ABC прямоугольный треугольник, ∠ С = 90°, CH- высота, AH = 2 см - проекция катета AC на гипотенузу, BH = 18 см - проекция катета BC на гипотенузу.
Найти катеты AC и BC.
Обозначим для удобства катеты AC = a, BC = b, проекции катетов AH = a₁, BH = b₁, высоту CH = h.
Высота в прямоугольном треугольнике, опущенная на гипотенузу, равна среднему пропорциональному проекций катетов на гипотенузу.
h² = a₁*b₁ = 2 * 18 = 36; h = 6
⇒ Высота треугольника, опущенная на гипотенузу CH = h = 6 см.
Из прямоугольного ΔACH по теореме Пифагора:
a² = h² + a₁² = 6² + 2² = 36 + 4 = 40; a = √40 = 2√10
Катет AC = 2√10 см/
Из прямоугольного ΔBCH по теореме Пифагора:
b² = h² + b₁² = 6² + 18² = 36 + 324 = 360; b = √360 = 6√10
Катет BC = 6√10 см.
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.
......................