хорда a=5√2 окружности стягивает дугу в 90 градусов - это значит, центральный угол , который опирается на эту дугу(хорду) равен 90 град
тогда отрезки (хорда +радиус+радиус) образуют прямоугольный равнобедренный треугольник с углом при вершине <O= 90 град ., здесь хорда-основание, радиусы - боковые стороны, углы при основании равны между собой <A=<B= (180-<O) /2 =(180-90) /2 =45град -тогда радиус окружности R =a/√2 = 5√2 /√2= 5
полный круг/окружность - это 360 град , тогда
длина дуги 90 град - 1/4 окружности 1/4*2п*R =п/2 *5 =5п/2
площадь сектора 90 град - 1/4 площади круга 1/4*пR^2=п/4 *25=25п/4
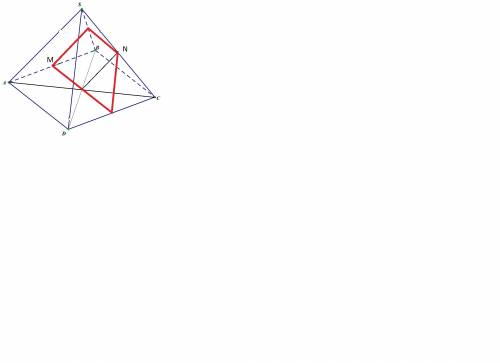
1) Так как по заданию дана правильная четырехугольная пирамида с равными рёбрами, то боковые грани такой пирамиды - это равносторонние треугольники.
Из точки N проводим прямую, параллельную SA, до пересечения с плоскостью основания. В треугольнике ASC это средняя линия, точка пересечения прямой из точки N - это центр основания, точка О.
Через точки М и О проводим след сечения заданной плоскости с основанием. Этот след пересекает ребро СД в его середине - в точке К.
Так как отрезок МК параллелен ВС (это линия пересечения боковой грани BSC и основания, то в грани BSC из точки N проводим прямую, параллельную ВС. Отрезок NP - это след сечения заданной плоскостью грани BSC.
Осталось соединить точки М и Р и сечение готово.
Оно представляет собой равнобокую трапецию. Основание её равно стороне основания пирамиды, а остальные стороны трапеции как средние линии треугольников боковых граней равны половине стороны основания.
2) Угол между прямыми SA и MN найдём методом параллельного переноса.
Перенесём отрезок MN точкой М в точку А, то есть на половину стороны основания. Тогда точка N при сдвиге на половину стороны основания переместится в середину бокового ребра CSD (на длину средней линии этой грани). Получим медиану треугольника АSD.
Так как боковая грань - равносторонний треугольник с углами по 60 градусов, то угол между ребром SA и медианой этой грани равен 30 градусов.
тк уголС=45, угол В=90, то угол А=45, из этого следует что треугольникАВС равнобедренный значит вессектриса BDбудет также медианой и высотой от сюда DC=DA=8
рассмотрим треугольник BCD угол C= 45 уголD= 90 соответственно Угол B=45 те данный треугольник равнобедренный, значитрастояние от точки D до середины BC будет медианой бессектрисой и высотой
рассмотрим треугольник NDC угол C =45 ,угол N=90,соответственно угол CDN=45,те данный треугольник раснобедренный. по теореме пифагора DC^2=2*DN^2
DN^2 =64\2=32
DN=5,65685(бесконечное число)
а) значит DN находиться между 5 и 6
б) треугольник AMD угол М=90 тк( DM перпендикулярно AB) угол А=45 соответственно угол ADM=45 те данный треугольник равнобедренный
по теореме пифагора AD^2=2*DM^2 DM^2=AD^2\2
DM^2=64\2=32
значит DM=DN
угол NDM будет смежним с углами NDC=45 и ADM=45значит угол NDM=90
из этого по теореме пифагора 2*DN^2=MN^2 из перечисленно выше примеров делаем вывод что MN^2=64 те MN=8
Подробнее - на -