Сначала немного рассуждений.
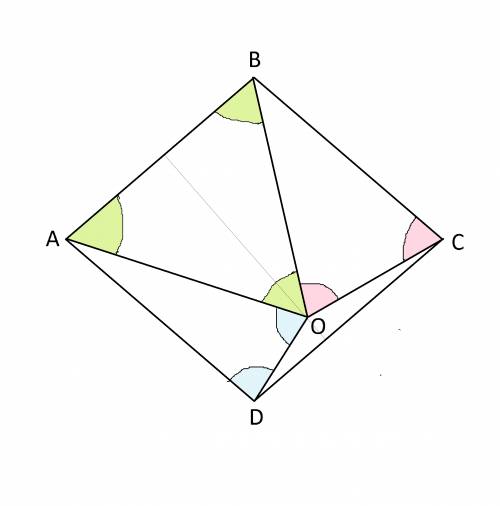
На стороне АВ вершиной внутрь ромба построен равносторонний треугольник.
Стороны этого треугольника равны сторонам ромба ( АВ - сторона ромба, у ромба все стороны равны, у равностороннего треугольника - тоже), а острый угол ромба больше 60°, иначе сторона АО построенного треугольника АОВ должна совпасть со стороной АD ромба.
Углы равностороннего треугольника равны 60°.
Сумма углов ромба, прилегающих к одной стороне, равна 180°.
Следовательно
∠DАО+∠СВО=180°-(ОАВ+ОВА)=180° -60°*2=60°
Рассмотрим треугольники DАО и СВО.
Они - равнобедренные, так как АВ=АD=АО=BO=ВС по условию задачи - стороны треугольника АОВ равны сторонам ромба и равны АВ.
Сумма всех углов ᐃ DАО и ᐃ СВО равна 180°*2=360°.
Углы в каждом из них при основаниях равны.
Сумма углов при основании ᐃ АОD+ cумма углов при основании ᐃ ВОС=
(360°- (∠DАО+∠СВО)=360°-60°)=300°
Сумма ∠DОА+∠ СОВ=300°:2=150°
Сумма всех углов при точке О равна 360°
Угол СОD=360-(∠АОD+ВОD)- АОВ=360°-150°-60°=150°
Дано: острый угол α и сторона a.
Построение:
1) Построим острый угол равный данному (рис. 1). Для этого:
1. Из вершины угла α проведём окружность с произвольным радиусом r. На луче OL построим окружность с центром в точке O и радиусом r.
2. С циркуля замерим расстояние (k) между точками пересечения окружности с углом α. Из точки пересечения окружности с лучом OL проведём окружность с радиусом k.
3. Проведём луч через начало исходного луча и одну из точек пересечения окружностей. Получим угол, равный углу α.
2) Построим первую вершину (A) квадрата (рис. 2), проведя параллельную прямую равноудалённую от одной из сторон угла на a (рис. 2). Для этого:
1. Проведём два перпендикуляра на одной стороне угла, для этого:
1.1. Из любой точки стороны угла проведём окружность произвольного радиуса v. В точках пересечения окружности со стороной угла, проведём окружности радиусом t, t > v. И соединим две точки пересечения окружностей с радиусом t. Так мы получили один перпендикуляр, аналогично получим и второй.
2. С циркуля отложим на этих перпендикулярах отрезки равные a, при этом они лежат в одной полуплоскости от стороны угла. Проведём прямую через концы отрезков, не лежащие на стороне угла. Точку пересечения этой прямой со второй стороной угла отметим, как A.
3) Построим вторую вершину (B)квадрата (рис. 3), проведя перпендикуляр из точки A на сторону угла, не содержащую эту прямую. Для этого:
1. Замерим расстояние m, с циркуля, между точками O и A. Из точки A проведём окружность с радиусом m. Из точек пересечения этой окружности с другой стороной угла (точки O и A₁), проведём окружности с радиусом m. Точки пересечения этих окружностей соединим прямой, которая и будет перпендикуляром.
2. Точку пересечения перпендикуляра со стороной угла, отличную от точки A, отметим точкой B.
4) Построим третью вершину (C) квадрата (рис. 4). Для этого:
1. С циркуля замерим длину a.
2. На луче OB, от точки B, отложим с циркуля отрезок a, второй его конец отметим точкой C.
5) Построим четвёртую вершину (D) квадрата (рис. 4). Для этого:
1. Из точек A и C проведём окружность радиусом a.
2. Одной точкой пересечения, будет точка B, а другую точку отметим, как D.
6) Соединим вершины A и B, B и C, С и D, D и A. Получили квадрат, 2 вершины которого принадлежат одной стороне угла α (вершины B и C), а третья (A) - другой.