Если квадрат и ромб имеют одинаковые периметры, тто они имеют и одинаковые стороны. Воспользуемся следующей формулой для вычисления площади параллелограмма в случае ромба.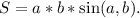 
В данном случае стороны равны, значит формула упрощается до 
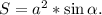. Заметим, что 
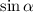Это угол между сторонами ромба. Здесь не имеет значения острый или тупой, так как в обоих случаях будет положительный ответ. Площадь квадрата же всегда равна 
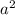. Заметим, что синус всегда меняется в данном случае от 0 до 1. То есть только в случае синуса равного 1 (а это квадрат) площадь ромба равна площади квадрата, в остальных случаях площадь ромба всегда меньше площади квадрата.
Центр описанной вокруг треугольника окружности находится в точке пересечения срединных перпендикуляров треугольника.
Треугольники АВD и BCD равны, т.к. параллелограмм делится диагональю ВD на два равных треугольника.
Радиусы описанных вокруг этих треугольников окружностей равны.
Проведем срединные перпендикуляры и найдем центры О и О1 описанных окружностей.
Соединив центры О и О1 с вершинами В и D параллелограмма, получим ромб
ВОDО1, т.к. его стороны - радиусы равных описанных окружностей, и диагонали пересекаются под прямым углом.
Его диагональ ОО1- искомое расстояние между центрами окружностей.
Угол ВОD центральный ( находится между двумя радиусами окружности с центром О) и равен удвоенному углу α, который является вписанным в эту окружность.
Сторона ромба = R
R=a:2 sin α
где а - диагональ BD параллелограмма
α — угол ромба, лежащий против стороны BD.
Ход решения:
1. Найти ВD по теореме косинусов
Найти сторону ОВ=R
Найти ОО1, диагональ ромба, - искомое расстояние - по формуле
d=a√(2-2·cos α)=a√(2+2·cosβ)