ответ:вот
Объяснение:
1) ∠М = 45°,
ΔАВО = ΔСМО по стороне и двум прилежащим углам
2)∠А₁ = 40°; ∠А₂ = 60°
3) ∠А = 70°
∠С = 50° (
∠В = 60°
Объяснение:
1) ВС = ОС (по условию)
∠ВОА = ∠МОС (как вертикальные при пересекающихся прямых )
и равны 180 - ∠АОС = 85°, следовательно ∠АВС = ∠АМС = 45°
ΔАВО = ΔСМО по стороне и двум прилежащим углам
2)
АН = высота на сторону ВС
(1) ∠В : ∠С = 5 : 3 ⇒ 3∠В = 5∠С (по условию))
(далее значки углов просто опустим)
(2) А -80 = В - С (по условию)
( 3) А+В+С = 180 (по свойству треугольника)
из (1) В = 5С/3
из (3) А = 180-В - С
подставим это в (2), получим 180 - 5С/3-С +80 = 5С/3 -С ⇒ ∠С = 30°
тогда ∠В = 50°,
∠А = 100°
тогда из треугольников АНС и АВН вычислим ∠А₁ = 40°; ∠А₂ = 60°
3)
∠А = 140/2 = 70° (равен половине дуги, на которую опирается)
∠С = 100/2 = 50° (аналогично)
∠В = 180-70-50 = 60°
дано: тр. АBC=тр. DEF.
AC=FD, CB=EF
По условию теоремы две пары отрезков этих треугольников равны между собой (АС = FD и СВ = EF). Углы между отрезками также равны (т.е. ∠АСВ = ∠EFD).
Доказать, что треугольник ABC равен треугольнику DEF.
Доказательство :Поскольку имеется равенство углов (∠АСВ = ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина С совпадала с вершиной F. При этом отрезки СА и СВ наложатся на отрезки FE и FD. А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED. Это в свою очередь даст совмещение вершин А и D, В и Е. Следовательно, треугольники полностью совместятся, а значит, они равны.
Доказательство для острого и тупого угла одинаково.
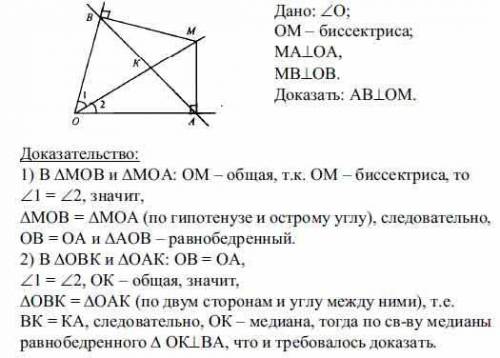
По условию ОМ - биссектриса, МА⊥ОА, МВ⊥ОВ =>
Треугольники АОМ и ВОМ прямоугольные, имеют общую гипотенузу ОМ и по равному острому углу ( ∠АОМ=∠ВОМ).
∆ АОМ=∆ ВОМ по 3-му признаку равенства прямоугольных треугольников. . Следовательно, их катеты АО=ВО, поэтому ∆ АОВ - равнобедренный .
В равнобедренном треугольнике биссектриса угла между равными сторонами - еще и медиана и высота.
Высота ОН⊥АВ, ОН принадлежит ОМ. ⇒
АВ⊥ОМ, ч.т.д.