0А=6см
Перпендикуляр и наклонные к
плосксти.
Объяснение:
Дано:
SA, SB - наклонные к
плоскости а
SO - перпендикуляр к а
SB=17см
ОВ=15см
SA=10см
------------------------------------
ОА - ?
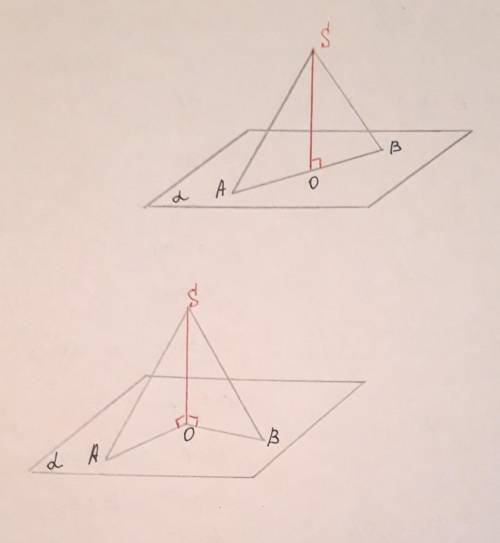
SO - перпендикуляр к плос
кости а ==> SO перпендику
лярна прямым ОВ иОА.
Возможны 2 варианта:
1) точки SAОB лежат в одной
плоскости;
2) точки SAОB не лежат в од
ной плоскости.
Решение и ответ одинаковы
для обоих вариантов.
Рассмотрим треугольник SOB:
<SOB=90°
Треуг. SOB - прямоугольный.
По теореме Пифагора:
SO^2=SB^2-OB^2
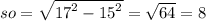
Рассмотрим треугольник SOA:
<SOB=90°
Треуг. SOA - прямоугольный.
По теореие Пифагора:
OA^2=SA^2-SO^2
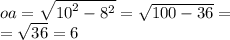
Oтвет:
ОА=6см

1) Проведём произвольно наклонную(ребро двугранного угла).По левую сторону от неё обозначим точку А и опустим из неё перпендикуляр на ребро в точку С1 . По правую сторону от линии ребра отмети м точку А1. Соединим её с точками А и С1. Получим прямоугольный треугольник АС1А1.(на чертеже углы выглядят произвольно). В данном треугольнике АС1=51 расстояние до ребра первой точки. АА1 расстояние от точки до другой грани. Угол АА1С прямой . Аналогично строим второй треугольник ВВ1С2. Эти треугольники подобны поскольку они прямоугольные (АА1 и ВВ1 перпендикулярны к грани) и уних общий линейный угол двугранного угла. Отсюда АА1/АС1=х/34. Где x расстояние до грани от другой точки. x=15*34/51=10.
2)10 сантиметров.
Объяснение:
из KN||AC и AK=KB мы узнаем, что KN является средней линией треугольника ABC.
т.к. KN - средняя линия, ее длина равняется половине АС, то есть 6 сантиметрам.
т.к. отрезок МК перпендикулярен плоскости треугольника АВС треугольник MKN является прямоугольным.
По теореме Пифагора MN^2=MK^2+KN^2
MN^2=6^2+8^2
MN^2=36+64
MN=10 см
АС = 14 см
ВС = 1/2 АС = 7 см
Катет напроти кута 30° = половина гипотинуза, из этого понятно, что
АС = х; ВС = 1/2х
значит
х + 1/2х = 21
1.5х = 21
х = 14 см
Значит АС = 14 см
а ВС 7см
На листке х + 2х потому что я АС взял за 2х, а ВС за 0.5 АС, тоесть за х