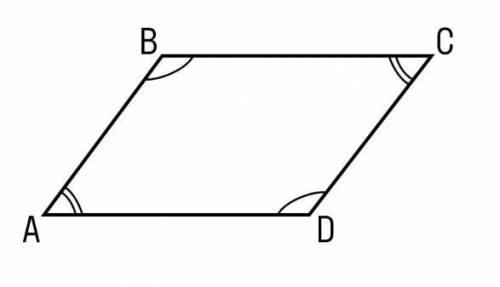
Противоположные углы параллелограмма равны между собой, сумма соседних углов равна 180°. ∠A=∠C; ∠B=∠D; ∠A+∠B=∠B+∠C=∠C+∠D=∠A+∠D=180°, если острый угол параллелограмма равен 52°, тогда остальные равны по: ∠А=52°; ∠В=∠D=180°-52°=128°; ∠A=∠C=52°; ∠B=∠D=128°.
Проверка: Сумма всех углов четырёхугольника равна 360°, то есть, должно выполниться равенство: ∠А+∠В+∠С+∠D=52°+128°+52°+128°=180°+180°=360°, равенство выполнено, значит, углы найдены верно. ответ: углы параллелограмма равны: 52°; 128°; 52°; 128°.
Пирамида MABCD, основание - прямоугольник ABCD: AD=BC=18 см; AB=CD=10 см; O- точка пересечения диагоналей AС и BD, MO - высота пирамиды. Так как у прямоугольника диагонали равны и точкой пересечения делятся пополам, то OA = OB = OC = OD - это проекции боковых ребер на основание. Проекции наклонных равны, следовательно, наклонные тоже равны : AM = BM = CM = DM - боковые ребра пирамиды. Тогда ΔAMD = ΔBMC - по трём равным сторонам, ΔAMB = ΔDMC - по трём равным сторонам. Проведем KT║AD ⇒ OK=OT=AD/2 = 18/2 = 9 смΔMOT - прямоугольный, теорема ПифагораMT² = MO² OT² = 12² 9² = 144 81=225 = 15²MT = 15 см см²Проведем FG║DC ⇒ OG=OF=DC/2 = 10/2 = 5 смΔMOF - прямоугольный, теорема ПифагораMF² = MO² OF² = 12² 5² = 144 25 = 169 = 13²MF = 13 см см²Площадь боковой поверхности пирамиды см²Sбок = 384 см²Площадь основания см²Площадь полной поверхности пирамиды S = 384 180 = 564 см²