ответ: ∠ВАС = ∠ВСА = 30 ° ; ∠АВС = 120° .
Условия задачи:
Δ АВС - равнобедренный , следовательно:
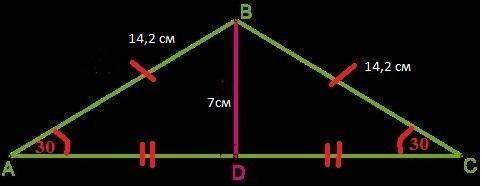
Боковые стороны равны ⇒ АВ=ВС = 14,2 см
Углы при основании равны :
АС - основание ⇒ ∠BAC (∠BAD) = ∠BCA (∠BCD)
BD =7,1 см - высота к основанию АС ⇒ является медианой и биссектрисой :
∠BDA = ∠BDC = 90° ( т.к. BD - высота)
AD = DC = АС/2 (т. к. BD - медиана)
∠ABD = ∠CBD (т. к. BD - биссектриса)
ΔBDA = ΔBDC - прямоугольные треугольники
Решение.
1) ΔBAD
По условию катет BD = 7,1 см , гипотенуза АВ = 14,2 см , следовательно :
BD = 1/2 * AB = 1/2 * 14,2 = 7,1 см
Если катет равен половине гипотенузы, то угол лежащий против этого катета равен 30° ⇒∠DAB (∠ BAC) = 30°
Проверим по определению синуса:
sin A = 7/14 = 1/2 ⇒ ∠BAC (∠BAD ) = ∠BCA (∠BCD) = 30°
2) ΔАВС :
Сумма углов любого треугольника = 180°
∠АВС = 180° - (∠ВАС + ∠ВСА)
∠АВС = 180 - 2*30 = 120 °
ответ: ∠ВАС = ∠ВСА = 30 ° ; ∠АВС = 120° .
Условия задачи:
Δ АВС - равнобедренный , следовательно:
Боковые стороны равны ⇒ АВ=ВС = 14,2 см
Углы при основании равны :
АС - основание ⇒ ∠BAC (∠BAD) = ∠BCA (∠BCD)
BD =7,1 см - высота к основанию АС ⇒ является медианой и биссектрисой :
∠BDA = ∠BDC = 90° ( т.к. BD - высота)
AD = DC = АС/2 (т. к. BD - медиана)
∠ABD = ∠CBD (т. к. BD - биссектриса)
ΔBDA = ΔBDC - прямоугольные треугольники
Решение.
1) ΔBAD
По условию катет BD = 7,1 см , гипотенуза АВ = 14,2 см , следовательно :
BD = 1/2 * AB = 1/2 * 14,2 = 7,1 см
Если катет равен половине гипотенузы, то угол лежащий против этого катета равен 30° ⇒∠DAB (∠ BAC) = 30°
Проверим по определению синуса:
sin A = 7/14 = 1/2 ⇒ ∠BAC (∠BAD ) = ∠BCA (∠BCD) = 30°
2) ΔАВС :
Сумма углов любого треугольника = 180°
∠АВС = 180° - (∠ВАС + ∠ВСА)
∠АВС = 180 - 2*30 = 120 °

1.
(рис.1)
Обозначим x = AD
AF = AD = x
CF = EC = 6
BE = BD = 1,5x
AB = AD + DB = x + 1,5x = 2,5x
BC = BE + EC = 1,5x + 6
AC = AF + FC = x + 6
P = AB + BC + AC = 2,5x + 1,5x + 6 + x + 6 = 5x + 12
5x + 12 = 52
5x = 40
x = 8
AB = 20 см
BC = 18 см
AC = 14 см
2.
(рис.1)
под трёхбуквенными обозначениями подразумевается угол
EDF = EDO + ODF = 90º - EDB + 90º - ADF
EDB = (180º - ABC)/2
ADF = (180º - BAC)/2
после преобразования получим
EDF = (ABC + BAC)/2
по аналогии
DEF = (ABC + ACB)/2
EFD = (BAC + ACB)/2
отсюда получаем углы 55º, 75º, 50º
3.
(рис.2)
P = r + r + 4 + 4 + 21 + 21 = 56
2r + 50 = 56
2r = 6
r = 3 см
Объяснение: