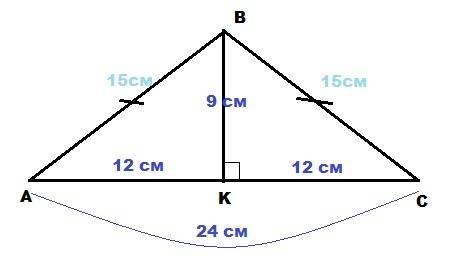
ΔABC - равнобедренный : AB = BC;
AC = 24 см; BK⊥AC; BK = 9 см
ВК - высота равнобедренного треугольника, она же и медиана ⇒
АК = КС = АС : 2 = 24 : 2 = 12 см
По теореме Пифагора из прямоугольного ΔВСК :
BC² = BK² + KC² = 9² + 12² = 225 = 15²
BC = 15 см ⇒ AB = BC = 15 см
Площадь треугольника АВС можно посчитать с трех разных формул
1) Через основание и высоту
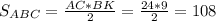 см²
см²
2) Через полупериметр и радиус вписанной окружности
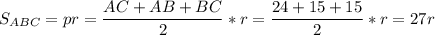
27r = 108 ⇒ r = 108 : 27 = 4 см
3) Через 3 стороны и радиус описанной окружности
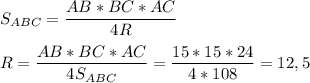
R = 12,5 см
ответ: радиус вписанной окружности r = 4 см;
радиус описанной окружности R = 12,5 см
Проведем прямую АК перпендикулярно AD (пусть К - точка пересечения АК с продолжением ВС, ясно, что АК - высота трапеции, АК = Н) и рассмотрим проекции точек K,L,P,F на эту прямую. К примеру, точка К делит отрезок, соединяющий А и середину ВС, в отношении 2/1, считая от А, поэтому её проекция на АК - пусть это точка K1, делит АК в отношении 2/1, считая от А. То есть АК1 = Н*2/3.
Аналогично AL1 = AK1 = H*2/3; AP1 = AF1 = H/3; L1, P1, F1 проекции L, P, F на АК.
Легко видеть, что проекция точки пересечения KP и LF на АК попадает в середину АК, то есть делит высоту пополам. От оснований ничего не зависит.
!используем теорему синусов для треугольника!
составляем отношения:
BC/sinA=AC/sinB=AB/sinC=2×R
=> AC= (BC×sinB)/sinA = 2 квадратный корень 6
ответ: АС=