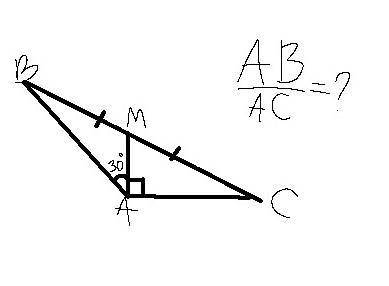
Смотрите на рисунок ...
У сторон АВ и АС общая вершина - А, и через неё и проведём медиану АМ к стороне ВС ...
Будем искать:
АС/АВ = ?
ИЛИ
АВ/АС = ?
Итак ...
Что можно сказать про медиану?
Она делит треугольник на два треугольника, площади которых равны ...
Получаем :
1) Площадь треугольника АВМ = площадь треугольника АМС.Рассмотрим треугольник ВМА.
Его площадь можно найти по вот такой формуле:
Площадь треугольника ВМА = ½*АВ*АМ*синус угла ВАМ
По условию угол ВАМ равен 30° ...
Площадь треугольника ВМА = ½*АВ*АМ*синус угла в 30°
Синус в 30° равен ½.
Получаем:
Площадь треугольника ВМА = ¼*АВ*АМ.
Теперь посмотрим на треугольник АМС.
Он прямоугольный... А площадь прямоугольного треугольника равна половине произведения его катетов. (В нашем случае АМ и АС - катеты).
Запишем вот так :
Площадь треугольника АМС = ½*АС*АМ..
ПО ВЫШЕ СКАЗАННОМУ В ПУНКТЕ 1 СЛЕДУЕТ, ЧТО :
½*АВ*АМ = ¼*АМ*АС
½*АВ = ¼*АС
АВ = ½*АС ...
Получаем :
АС/АВ = АС/(½*АС) = 1 : ½ = 2.
АВ/АС = (½*АС)/АС = ½.
(ЕСЛИ НЕВЕРНО ОТМЕТЬТЕ КАК НАРУШЕНИЕ!)
В ΔАВС найти периметр и длины медиан, если А(3/2 ;1;-2) , В(2;2;-3) , С(2;0;-1).
Объяснение:
а)d=√( (х₁-х₂)²+(у₁-у₂)²+ (z₁-z₂)²), где (х₁;у₁; z₁), (х₂;у₂; z₂) -координаты концов отрезка.
АВ=√( (2-1,5)²+(2-1)²+ (-3+2)²)=√( 0,25+1+1)=√2,25=1,5 ;
АС=√( (2-1,5)²+(0-1)²+ (-1+2)²)=√( 0,25+1+1)=√2,25=1,5 ;
ВС=√( (2-2)²+(0-2)²+ (-1+3)²)=√( 0 +4+4)=√8=2√2.
Р=АВ+АС+ВС , Р=3+2√2.
б) х=(х₁+х₂):2 ,у=(у₁+у₂):2 , z=(z₁+z₂):2, где (х₁;у₁), (х₂;у ₂), (z₁;z₂), координаты концов отрезка , (х;у ;z), -координаты середины.
К-середина СВ. Координаты К( (2+2):2 ; (0+2):2 ;(-1-3):2 ) или К(2;1;-2)
АК=√( (2-1,5)²+(1-1)²+ (-2+2)²)=√( 0,25 +0+0)=√0,25=0,5.
М-середина АС. Координаты М( 1,75; 0,5 ;-1,5) ,
ВМ=√( (1,75-2)²+(0,5-2)²+ (-1,5+3)²)=√( 0,0625 +0,25+2,25)=√2,5625,
Р-середина АВ. Координаты Р( 1,75; 1,5 ;-2,5) ,
СР=√( (1,75-2)²+(1,5-0)²+ (-2,5+1)²)=√( 0,0625 +2,25+2,25)=√4,5625.