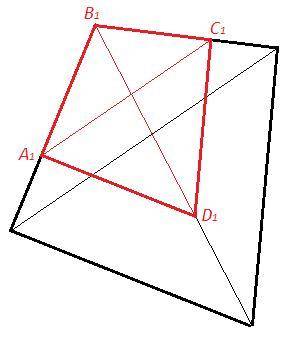
Соответствующие диагонали разбивают подобные многоугольники на подобные треугольники.
Доказываем подобие треугольников (с одинаковым коэффициентом и соответствием сторон) - тем самым доказываем подобие многоугольников.
(3) A1B1C1~ABC, A1D1C1~ADC (по двум сторонам и углу между ними)
(4) A1B1C1~ABC (по данным смежным сторонам и углу между ними)
A1D1C1~ADC (по стороне (A1C1, AC) и прилежащим углам)
(6) A1B1C1~ABC, A1B1D1~ABD (по трем пропорциональным сторонам)
∠C1A1D1=∠CAD
C1A1D1~CAD (по двум сторонам и углу между ними)
Пусть трапеция ABCD, BC - меньшее основание, AD - большее, AB - боковая сторона с прямыми углами. Тогда углы ADC и ACB по условию равны и равны 60 градусов.
Средняя линия равна полусумме оснований, т.е. (BC+AD)/2. Надо найти её отношение к BC, а значит выразить AD через BC или наоборот.
Если угол ACB равен 60 градусов, то и угол CAD тоже (не помню верный термин, но потому что AD и BC параллельны). Раз ADC и CAD равны 60, то и ACD равен 60, а значит треугольник ACD - равносторонний. Сторона CD, таким образом, равна AD (и равна AC, но это, как мы увидим, неважно).
Опустим из точки C перпендикуляр к основанию AD, допустим в точку H. Если угол CDH равен 60 градусов, то угол DCH будет 30 градусов. Известно, что против угла в 30 градусов лежит сторона, равная половине гипотенузы. Гипотенуза - CD, и мы узнали что она равна AD. То есть DH = 1/2 CD = 1/2 AD, или, иначе говоря, этот перпендикуляр делит нижнее основание пополам.
В то же время AH = BC, то есть BC = 1/2 AD, или AD = 2 BC
Мы выразили одно основание через другое, подставляем в искомое соотношение:
((BC + AD)/2 ) / BC = (BC + 2 BC) / 2BC = 3/2
Спрашивайте, если что непонятно