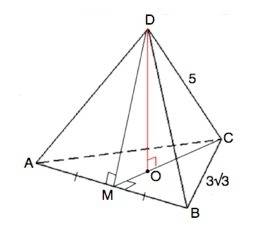
Одна из формул площади треугольника S-h•a/2
S (MDC)=DO•CM/2 ( DO - высота, СМ - основание треугольника)
∆ АВС правильный, -- все углы равны 60°
Медиана правильного треугольника является его биссектрисой и высотой.
СМ⊥АВ
СМ=СВ•sin60°=3√3•√3/2=4,5
Вершина правильной пирамиды проецируется в центр основания ( для правильного треугольника в основании - точку пересечения медиан)
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины.
СО=4,5•2/3=3
∆ DCO египетский, ⇒ DO=4
S (MDC)=4•4,5:2=9 см²
Два ПОДОБНЫХ, но НЕРАВНЫХ треугольника имеют две пары РАВНЫХ сторон.
Эти стороны, естественно, не соответственные, то есть в подобных треугольниках АВС и ХYZ, если сторона АС=9, то соответственная ей сторона XZ=6см, а стороне АВ=6см соответствует сторона XY. Стороне же ВС соответствует сторона YZ=9см. (Так как стороны одного треугольника ОБЯЗАТЕЛЬНО должны быть БОЛЬШЕ соответственных сторон другого - они же ПОДОБНЫЕ).
Тогда коэффициент подобия треугольников будет равен АС/XZ=9/6=3/2. Найдем оставшиеся стороны из подобия треугольников:
АВ/XY=3/2 или 6/XY=3/2, отсюда XY=4см
ВС/YZ=3/2 или ВС/9=3/2, отсюда ВС=13,5см.
ответ: стороны аервого треугольника АВ=6см, ВС=13,5см, АС=9см.
Соответственные стороны другого (подобного) треугольника равны
XY=4см, YZ=9см, XZ=6см.