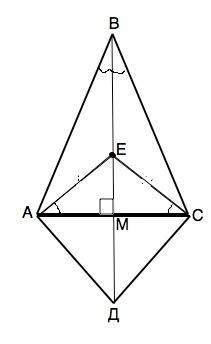
Рассмотрим ∆ АВД и СВД.
Стороны АВ=ВС, АД=ДС по условию, ВД - общая.
∆ АВД=∆ СВД
Пусть М – точка пересечения ВД и АС.
Из доказанного выше равенства треугольников следует равенство их углов: ∠АВД=∠СВД. и ∠АДВ=∠СДВ.
Следовательно, ВМ - высота, биссектриса и медиана равнобедренного ∆ АВС, и ДМ - высота, биссектриса и медиана ∆ АДС.
АМ=СМ, ВД– срединный перпендикуляр к АС. Все его точки равноудалены от А и С (свойство), поэтому
∆ АЕС –равнобедренный, и углы при основании АС равны независимо от места нахождения Е на ВД. Доказано
Объяснение: Пусть дана треугольная призма, в основании которой лежит прямоугольный треугольник с катетами 8 см и 15 см.
Площадь большей боковой грани равна 102 см².
Вычислим высоту призмы.
По теореме Пифагора ищем гипотенузу : √8^2+15^2=√289=17 см.
Найдём высоту призмы : большая боковая грань равная 102 см². по условию образуется гипотенузой и высотой, значит 102 / 17=6 см.