Ромб - это параллелограмм, у которого все стороны равны (докажите сами). То есть ромб является параллелограммом.
<AOE = <ACB (как соответственные углы при ||-ных прямых OE и BC и их секущей AC).
Тогда треугольники ACB и AOE подобны по двум углам (<A=<A, <AOE=<ACB),
тогда их стороны пропорциональны, то есть:
AC/AO = BC/EO = AB/AE. (*)
Треугольники AOB и COD равны (докажите сами), тогда
AO = CO, тогда
AC/AO = (AO+CO)/AO = 2AO/AO = 2.
Тогда из (*):
2 = BC/EO, отсюда EO = (1/2)*BC,
Но у ромба все стороны равны, то есть BC = DC, поэтому
EO = (1/2)*BC = (1/2)*DC.
Ч. т. д.
ответ: 80.
Объяснение:
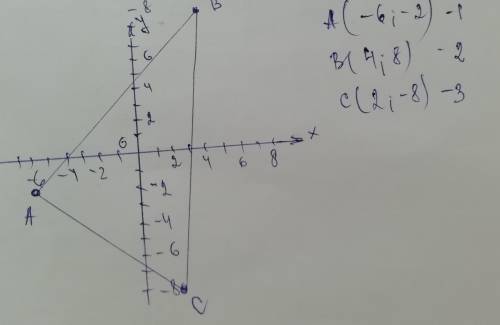
Построим координатную плоскость и нанесем точки А,В,С. (смотри чертёж).
Чтобы найти площадь при таких данных, воспользуемся формулой Герона:
S = √p(p-a)(p-b)(p-c), где a, b и c - стороны треугольника р=(a+b+c)/2 - полупериметр треугольника.
Но есть более простая формула:
S=1/2|(x2-x1)(y3-y1)-(x3-x1)(y2-y1|); (| | - по модулю);
Обозначим точки 1 - А; 2 - В; 3 - С.
Тогда S= 1/2| (4-(-6))(-8-2)-(2-(-6))(8-(-2))|=1/2| (10*(-6))-(10*10)|=1/2| (-60-100) |= 1/2 |-160|=1/2* 160=80.
80см2
Объяснение:
Пусть x-коэффициент пропорциональности, тогда меньшая сторона будет-2x, а большая-5x. Составим и решим уравнение:
2x+5x+2x+5x=56
14x=56
x=4
Меньшая сторона=2×4=8см
Большая сторона=2×5=10см
S=8×10=80см2