QS=54
Объяснение:
Новое решение.
Исходя из суммы углов треугольника, в треугольнике RPQ угол при верщине R = 30 градусам. Что означает, что в прямоугольном треугольнике RPQ катет равен половине гипотенузы, то есть RP=2*PS=36.
Аналогично в треугольнике RPQ угол Q=30 градусов, а значит гипотенуза PQ=2*RP=72.
Следовательно QS=PQ-PS=72-18=54
Старое решение:
Исходя из суммы углов треугольника, угол при верщине Q = 30 градусам. Тогда из треугольника tg60=RS/PS, а tg30=RS/QS
RS=tg60*PS
RS=tg30*QS
tg60*PS=tg30*QS -> QS=(tg60*PS)/tg30=tg60*ctg30*PS
т.к. tg a * ctg b =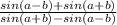 
тогда Q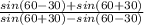S=
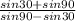*PS=
*PS=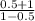
*PS=(1.5/0.5)*PS=3*PS
QS=3*18=54
8 см
Объяснение:
Пусть дан треугольник АВС. АС=30см. Обозначим точки касания вписанной окружности и сторон треугольника АС, АВ и ВС соответственно К, Т, Р.
Тогда по условию задачи ВТ=12 см и АТ=14 см
Тогда АТ=АК= 14 см
КС= АС-АК=30-14=16 см
КС=РС=16 см
ВР=ВТ=12 см
Тогда АВ=АТ+ВТ=12+14=26 см, ВС =ВР+РС=12+16=28 см
Тогда периметр Р= 26+28+30=84 см
Тогда полупериметр р=Р:2=84:2=42
Тогда площадь треугольника по теореме Герона
S=sqrt(p*(p-a)*(p-b)*(p-c))= sqrt(42*12*14*16)=336
С другой стороны площадь треугольника может быть вычислена по формуле S=p*r=42*r=336
=> r=336/42
r=8