АВСД -ромб. Диагонали ромба перпендикулярны и точкой пересечения делятся пополам. В треугольнике ВМД ВМ=МД, ВО=ОД, МО - общая сторона. Треугольники МОВ=МОД, треугольник ВМД равнобедренный. По тем же основаниям треугольник АМС равнобедренный. МО является высотой обоих треугольников, перпендикулярна ВД и АС. Если прямая перпендикулярна двум пересекающимся прямым в плоскости, то она перпендикулярна этой плоскости. ⇒ МО⊥ плоскости ромба и плоскости треугольника АВС, принадлежащего этой плоскости, что и требовалось доказать.
Треугольники АВF и АСF равны (это прямоугольные треугольники, у которых равны гипотенузы АВ и АС (как касательные из одной точки к окружности) и общий катет АF. Значит Sabf=Sacf. Если Sdecf = Sabd, то Sfbd= Seda. Тогда Scbe=Sabe (из равных площадей вычитаем равные площади, значит оставшиеся площади равны). В треугольнике АВС отрезок ВЕ, проведенный из вершины угла В к противоположной стороне, делит площадь этого треугольника пополам, так как Sabe и Sbec состоят из равновеликих частей (Sabd+Sade)=(Sbdf+Sdecf). Следовательно, ВЕ - медиана треугольника АВС. Рассмотрим <CВD и <АВЕ. Эти углы равны, так как <CВD вписанный, опирающийся на дугу СD, а <ABD (<ABE) - угол, образованный касательной к окружности и секущей, равен половине дуги ВD. Но дуги CD и BD равны (так как равны центральные углы ВОD и СОD, опирающиеся на эти дуги), значит <CВЕ и <АВЕ равны. Следовательно, ВЕ - биссектриса угла СВА. Но если в треугольнике АВС биссектриса и медиана совпадают, значит этот треугольник равнобедренный и стороны СВ и ВА равны. Но мы знаем, что ВА=АС, как касательные к окружности, проведенные из одной точки. Значит треугольник АВС равносторонний и <ВСА = 60°. <OCA = 90° (радиус к касательной в точку касания), тогда <OCB = <OCA-<BCA=90°-60° = 30°. ответ: угол ОСВ = 30°
т.к. AB- высота, то ∠ABC=90°
т.к. ∠ABC=90°, тогда ΔABC - прямоугольный
Найдем сторону AB по теореме Пифагора
AB=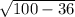
AB=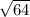
AB= 8
т.к. ∠D = 45°, а ∠ABC=90°, тогда ∠ BAC = 45° и значит Δ ABC - равнобедренный и стороны AB и BD равны, т.е. BD + CB=8+6=14
ответ: 14