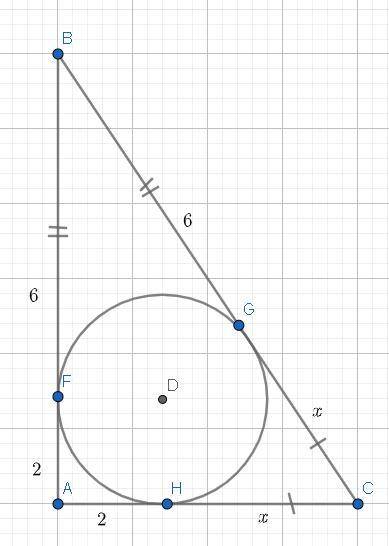
В случае окружности, вписанного в прямоугольный треугольник — точки касания делят все стороны на некие равные отрезки.
То есть: Через точку B — проведены 2 касательные: катет BA & гипотенуза BC.
В точках касания — отрезки друг другу равны(теорема о 2 касательных, проведённых с одной точки), тоесть: BF == BG.
BF == BG ⇒ BF == BG = 6.
Одни и те же действия с отрезками FA & AH, они тоже друг другу равны, так как их касательные проведены с одной точки.
FA == AH = 2.
Точно так же с отрезками HC & GC: HC == GC = x.
По теореме Пифагора:
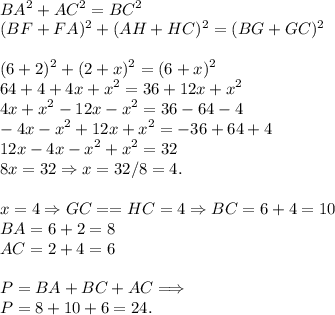
Вывод: P = 24 см.
1. Сумма внутренних углов треугольника 180
Угол BAC=180-90-60=30*
У нас есть теорема, что катет лежащий протий угла 30* , равен половине гипотенузы , значит BC=10:2=5 см
ответ: BC= 5см
2. Сумма углов треугольника 180*
Угол DCB = 180-45-90=45*
Значит треугольник BCD равнобедренный , CD=DB=8см
Угол С 90* , а угол DCB=45*, значит ACD тоже 45*
Значит CD- биссектриса , но она в то же время и высота , а значит это равнобедренный треугольник . Но в равнобедренном треугольнике высота=медиана =биссектриса. Если CD Медиана , то AD=DB .
DB=8см, значит AD тоже 8 см
АВ=8+8=16см
3.сумма внутренних углов треугольника 180*
угол EBC= 180-60-90=30*
Катет лежащий против угла 30* равен половине гипотенузы , а значит EB= 7*2=14 см ABC=180-30-90=60*
Угол ABE=ABC- EBC=60-30=30*
EAB=ABE=30* , значит ABE равнобедренный
Следовательно , AE=EB=14см
ответ : AE=14 см