™ Zmeura1204
Объяснение:
1)
∆LAE=∆FBG=∆HCI=∆JDK
∆LAE- равнобедренный прямоугольный треугольник
АЕ=LE/√2=2√2/√2=2см.
АВ=2*АЕ+ЕF=2*2+2√2=4+2√2 см.
Р(ABCD)=4*AB=4(4+2√2)=16+8√2 см
ответ: Р(ABCD)=16+8√2см.
2)
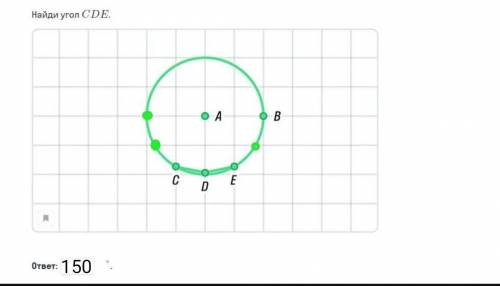
В окружность вписанный двенадцатиугольник.
Формула нахождения градусной меры угла.
180°(n-2)/n, где n=12 количество углов.
180°(12-2)/12=1800/12=150°
ответ: ∠СDE=150°
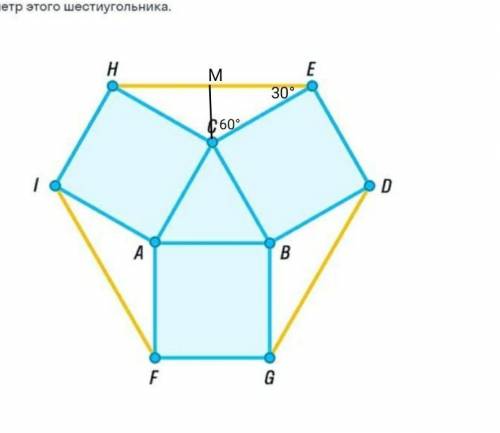
3)
В равностороннем треугольнике все углы по 60°
∠АСВ=60°
В квадрате все углы по 90°
∠ЕСВ=90°; ∠НСА=90°
Полный угол равен 360°
∠НСЕ=360°-∠ЕСВ-∠НСА-∠АСВ=
=360°-90°-60°-90°=120°
∆НСЕ- равнобедренный треугольник
НС=СЕ, стороны квадрата.
Сумма углов в треугольнике равна 180°
В равнобедренном треугольнике углы при основании равны
∠НЕС=(180°-∠НСЕ)/2=(180°-120°)/2=30°
СМ- высота, медиана и биссектрисса равнобедренного треугольника ∆НСЕ
∆СМЕ- прямоугольный треугольник.
cos∠MEC=ME/CE
cos30°=√3/2
√3/2=ME/4
ME=4√3/2=2√3см
НЕ=2*МЕ=2*2√3=4√3 см.
Рз.ф.=3*ЕD+3*HE=3*4+3*4√3 =12+12√3см
ответ: 12+12√3см
Обозначение:
Рз.ф.-периметр заданной фигуры.
В любой правильный многоугольник можно вписать единственную окружность.
Доказательство:
Надо доказать, что существует точка, равноудаленная от сторон многоугольника.
Пусть О - центр окружности, описанной около правильного многоугольника.
Тогда ОА₁ = ОА₂ = ОА₃ = ... как радиусы описанной окружности, значит треугольники ОА₁А₂, ОА₂А₃ и т.д. равны по трем сторонам (отрезки А₁А₂, А₂А₃ и т.д. равны, как стороны правильного многоугольника),
но тогда равны и высоты этих треугольников, проведенные к сторонам А₁А₂, А₂А₃ и т.д.
Значит, точка О равноудалена от сторон многоугольника, и окружность с центром в точке О и радиусом, равным ОК₁, пройдет через точки К₁, К₂, и т.д., то есть будет касаться сторон многоугольника и значит будет вписанной.
В правильном многоугольнике центры вписанной и описанной окружностей совпадают.
Докажем, что эта окружность единственная.
Предположим, что существует еще одна окружность с центром в некоторой точке О₁, вписанная в тот же правильный многоугольник.
Тогда точка О₁ равноудалена от сторон этого многоугольника, значит лежит в точке пересечения биссектрис его углов, значит совпадает с точкой О - точкой пересечения его биссектрис. Радиус этой окружности равен расстоянию от точки О до сторон, т.е. равен ОК₁, значит эти окружности совпадают.