6. Дано: ΔАВС, СР-биссектриса, АР=4 см, ВР=5 см
Найти: Периметр ΔАВС
1. СР- биссектриса ΔАВС => АР:ВР=АС:ВС
4:5=10:ВС
ВС=(5*10):4=12,5 (см)
2. Р(АВС)=АВ+ВС+АС=(АР+ВР)+ВС+АС
Р(АВС)=4+5+12,5+10= 31,5 (см)
ответ: 31,5 см
Объяснение:
7. Позначимо ромба АВСD, АВ = 5см, О - точка перетину діагоналей АС і ВD, АС = 6см. Знайти висоту АК
Розв"язання:
Діагоналі ромба рівні, звідси, АО = СО = АС/2=6/2=3, ВО = ОD
З прямокутного трикутника АВО( кут АОВ = 90 градусів):
За т. Піфагора
Звідси, діагональ ВD = 2ВО = 2*4= 8см.
Знаходимо полщу ромба
Тоді висота ромба дорівнює:
Відповідь: 4.8 см.
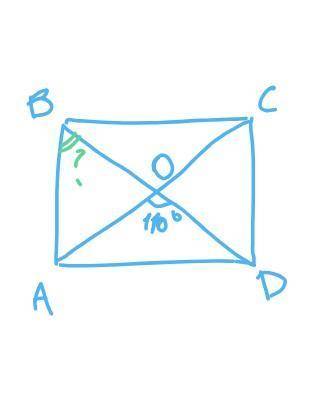
Диагонали прямоугольника имеют одинаковую длину, AC = BD;
Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам,
AO = OC = BO = OD;
Получается, треугольник ABO — равнобедренный (BO = AO), углы при основании равнобедренного треугольника равны, ∠ABO = ∠OAB;
∠ABD — это тот же ∠ABO;
∠AOB + ∠AOD = 180° (лежат на одном развёрнутом угле BOD), ∠AOB = 180° – ∠AOD = 180° – 110° = 70°;
Сумма углов треугольника равна 180°,
∠ABO + ∠AOB + ∠OAB = 180°,
Подставляем, что ∠ABO = ∠OAB, получаем
2 × ∠ABO + ∠AOB = 180°,
2 × ∠ABO = 180° – ∠AOB = 180° – 70° = 110°,
∠ABO = 110° ÷ 2 = 55° = ∠OAB
ответ: 55°
Нет, т.к. следуя теореме о неравенстве треугольника(каждая сторона треугольника меньше суммы двух других сторон). Проверим:
4<3+8
3<4+8
8>3+4 Как видим, это не подходит под формулу AB<AC+BC
Значит треугольник невозможен