2) ΔАВС , АМ, СК ВД - медианы, пересекаются в точке О , ∠АОС=90° ,
АС=12 см . Найти: ВД .
ΔАОС - прямоугольный, ОД - медиана , проведённая из прямого угла АОС . Она равна половине гипотенузы АС, то есть ОД=12:2=6 см.
Медианы в точке пересечения делятся в отношении 2:1, считая от вершины, то есть ВО:ОД=2:1 . Значит, ВО=2·ОД=2·6=12 см .
Вся медиана ВД=ВО+ОД=12+6=18 см
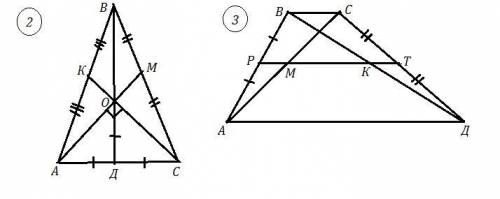
3) АВСД - трапеция , ВС║АД , РТ - средняя линия трапеции ,
АС ∩ РТ= М , ВД ∩ РТ = К , ВС=4 см , АД=12 см . Найти МК .
Рассм. ΔАВС , РМ - средняя линия, РМ=0,5·ВС=0,5·4=2 см .
Рассм. ΔАВД , РК - средняя линия , РК=0,5·АД=0,5·12=6 см .
МК=РК-РМ=6-2=4 см .
ответ: 64 см.
Объяснение: Малая диагональ делит ромб с углами A/B/C/D на 2 треугольника с противоположными углами 60°. Обозначим их A и C. Вычтя из 360°- 60°- 60°= 240° получим сумму 2-х других углов B и D. Поделив 240°/ 2 = 120° находим величину B и D второй пары противоположных углов. Малая диагональ является биссектрисой углов B и D и делит их пополам - 120°/ 2 = 60°. Отсюда все углы треугольников ABD и CDB равны 60°. Диагональ DB является общей стороной равносторонних треугольников ABD и CDB и равна 16 см Значит все стороны ромба равны 16 см. Периметр равен 16 × 4 = 64 см.
Сторона 16/4 = 4, площадь 4*4*sin(60) = 8*корень(3);
я заметил, что тут уже есть точно такое же решение этой задачи, и я так понял, что оно чем-то не устраивает.
На самом деле можно вот что сделать - разбить ромб на 2 равносторонних треугольника со стороной 4 (раз угол 60 радусов, то малая диагональ будет такой же, как сторона) теперь в этом треугольнике надо найти высоту (все равно какую). поскольку высота в нем совпадает с биссектрисой и медианой из то же вершины, то она образует с боковой стороной и ПОЛОВИНОЙ основания прямоугольный треугольник. Считаем её длину по теореме Пифагора :
Высота равна корень(4^2 - 2^2) = 2*корень(3);
Теперь считаем площадь ОДНОГО треугольника, это будет (1/2)*4*2*корень(3),
то есть 4*корень(3); поскольку ромб разрезан на 2 треугольника, ответ будет
8*корень(3);