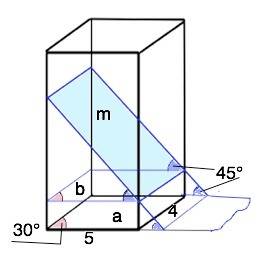
Пусть плоскость m - искомая.
Тогда плоскость а основания является её ортогональной проекцией на плоскость, содержащую основание призмы.
Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекции.
S (a)=S(m)•cos45°⇒
S(m)=S(a):cos45°
Формула площади параллелограмма
S=a•b•sinα, где а и b стороны параллелограмма, α - угол между ними.
S(a)=4•5•sin30°=20•1/2=10 дм²
cos45°=√2/2 или иначе 1/√2
S(m)=10:(1/√2)=10√2 см²
13) Высота, проведённая к основанию равнобедренного треугольника является так же медианой и бессектриссой
14) Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
15)Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
16) если три стороны одного треугольника равны трем сторонам другого треугольника то они равны
17)Окружность — геометрическое место точек плоскости, удалённых от некоторой точки — центра окружности — на заданное расстояние, называемое радиусом окружности
18) точка, от которой любые две данные точки, принадлежащие окружности, удалены на равные расстояния.
19) радиус- не только величина расстояния, но и отрезок, соединяющий центр окружности с одной из её точек.
20)Отрезок который проходит через центр окружности и соединяет две точки окружности
21)Отрезок, соединяющий две точки окружности, называется хордой.