Проанализируем каждое утверждение.
В равнобедренном треугольнике действительно равны углы при основании. Это утверждение верно.ответ: утверждение 1 верно.
Медианы треугольника пересекаются в одной точке - в центроиде (в центре тяжести треугольника). Она является одной из замечательных точек треугольника. Это утверждение верно.ответ: утверждение 2 верно.
Медиана произвольного равнобедренного треугольника, проведённая к ОСНОВАНИЮ, а не к боковой стороне, является его биссектрисой и высотой. Это утверждение неверно.ответ: утверждение 3 неверно.
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны. Это один из признаков равенства треугольников. Это утверждение верно.ответ: утверждение 4 верно.
ответ: 3).1)Треугольники подобны ⇒ и у другого треугольника стороныотносятся как 3х/4х/5х. Большая сторона - 5х, и она равна 15.
15=5х
х=3
тогда первая сторона 3х=9, вторая 4х=12
Периметр равен:9+12+15=36
ответ:36
2)Больший катет лежит против большего отрезка гипотенузы. По свойству катет в прямоугольном треугольнике есть среднее геометрическое между гипотенузой (16+9=25см) и его проекцией на гипотенузу (16см)
х=√(25*16)=20см
ответ:20см
3)Рисунок внизу.
В ΔABD по теореме косинусов:
cosABC=(AB²+BD²-AD²)/(2AB*BD)=(16+1-12,25)/(2*4*1)=4,75/8
В ΔABC по теореме косинусов:
AC²=AB²+BC²-2*AB*BC*cosABC=16+256-2*4*16*4,75/8=196
AC=14
ответ:14
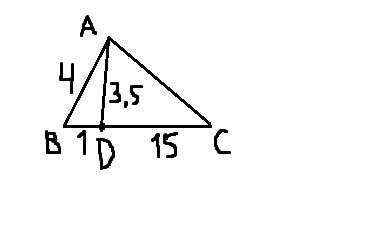
Достраиваем треугольник до прямоугольника, медиана в нем - это половина диагонали, а диагонали в прямоугольнике равны.
Это все доказательство :)))