Вариант решения.
ответ: 10 (ед. длины)
Объяснение:
Одна из формул площади параллелограмма
S=a•b•sinα, где а и b стороны с общей вершиной, α - угол между ними.
Ромб - параллелограмм с равными сторонами.
S=a•a•0.8=320 ⇒ a²=320:0,8=400 ⇒ a=√400=20. ⇒ АВ=ВС=20
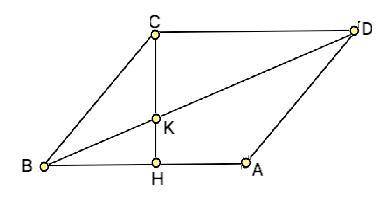
Опустим высоту СН. Из ∆ СВН высота ромба СН=СВ•sinB=20•0,8=16
По т.Пифагора ВН=√(BC²-CH²)=12
Примем длину СК=х. Тогда КН=16-х.
Прямоугольные треугольники ВКН и СКD подобны по равному острому углу при К. Из подобия следует отношение:
СD:BH=CK:KH
20:12=x:(16-x)
Решив уравнение, получим х=10.
СК=10 ( ед. длины)
теорема. прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.
рассмотрим следующий рисунок.
ah - перпендикулярен плоскости α. am это наклонная в плоскости α; a - прямая, проведенная в плоскости α через точку м перпендикулярно к проекции hm наклонной. теперь, докажем, что прямая а перпендикулярна ам. для этого рассмотрим плоскость amh.
по условию прямая а перпендикулярна нм. также прямая а перпендикулярна ан, так как ан перпендикулярна плоскости α. прямые нм и ан принадлежат плоскости анм и пересекаются. из этих трех пунктов следует, что прямая а перпендикулярна плоскости амн, значит, она перпендикулярна любой прямой, которая принадлежит плоскости амн.
так как прямая ам принадлежит плоскости амн, значит прямая a и прямая ам перпендикулярны между собой. что и требовалось доказать.
так как в теореме присутствуют три перпендикуляра, ан, нм и ам, теорема называется теоремой о трех перпендикулярах. все три прямых угла показаны на рисунке, который в начале доказательства. помимо основной теоремы о трех перпендикулярах, существует и обратная теорема о трех перпендикулярах.
обратная теорема
прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции.
. отрезок ad перпендикулярен к плоскости равнобедренного треугольника авс. известно, что ав = ас = 5см, вс = 6 см, ad = 12 см. найти расстояние от точки а до прямой вс.
решение.
пусть точка е это середина вс. тогда вс будет перпендикулярным ае. то есть ае будет расстояние от точки а до прямой вс.
еа является проекцией de на плоскость авс. ае перпендикулярен вс, а следовательно по теореме о трех перпендикулярах de будет перпендикулярен bc. получаем, что de - это расстояние от точки d до отрезка bc. теперь будем определять ae.
ве = (1/2)*вс = 3 см.
так как треугольник аве прямоугольный, то можем по теореме пифагора найти ае.
ае^2 = ab^2-be^2 = 25-9 = 16, следовательно, ае = 4 см.
ответ. 4 см.
Все стороны ромба равны, AB=BC
S(ABCD) =AB*BC*sinB => 320 =BC^2 *0,8 => BC=20
CH - высота, KCB=90
Диагонали ромба являются биссектрисами углов, KBC=B/2
tg(KBC) =tg(B/2) =CK/BC
sinB=4/5, cosB=3/5
tg(B/2) =sinB/(1+cosB) =1/2
CK/20 =1/2 => CK=10