Дан треугольник, две стороны которого равны по 10 см, третья - 12 см. Этот треугольник равнобедренный. Обозначим его АВС, АВ=ВС. Проведем высоту ВН к основанию. Высота равнобедренного треугольника, проведенная к основанию, является его медианой. ⇒ АН=СН=6 см. По т.Пифагора ВН=√(АВ²-АН²)=√(100-36)=8 см. Высоты к боковым сторонам равнобедренного треугольника равны. Найдем их из площади ∆ АВС.
Ѕ(АВС)=АС•ВН:2=48 см² В то же время Ѕ(АВС)=СМ•АВ:2, поэтому СМ•10:2=48 см², откуда СМ=АК=96:10=9,6 см.
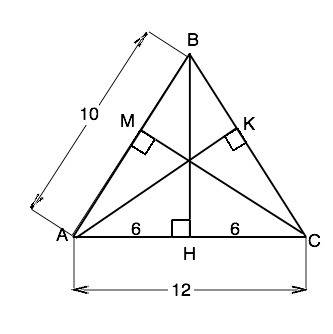
Дан треугольник, две стороны которого равны по 10 см, третья - 12 см. Этот треугольник равнобедренный. Обозначим его АВС, АВ=ВС. Проведем высоту ВН к основанию. Высота равнобедренного треугольника, проведенная к основанию, является его медианой. ⇒ АН=СН=6 см. По т.Пифагора ВН=√(АВ²-АН²)=√(100-36)=8 см. Высоты к боковым сторонам равнобедренного треугольника равны. Найдем их из площади ∆ АВС.
Ѕ(АВС)=АС•ВН:2=48 см² В то же время Ѕ(АВС)=СМ•АВ:2, поэтому СМ•10:2=48 см², откуда СМ=АК=96:10=9,6 см.

Окружность.
Точка О - центр данной окружности.
Отрезки КТ и ТЕ - хорды.
∠КОТ = 130°.
∪ТЕ = 110°.
Найти :∪КЕ (фиолетовой) = ?
Решение :∠КОТ - центральный (по определению центрального угла).
Градусная мера дуги, на которую опирается центральный угол, равен градусной мере соответствующего центрального угла.Следовательно -
∪КТ = ∠КОТ = 130°.
Сумма дуг с общими концами равна 360°.Следовательно -
∪КЕ (фиолетовая) + ∪КТ + ∪ТЕ = 360°
∪КЕ (фиолетовая) = 360° - ∪КТ - ∪ТЕ
∪КЕ (фиолетовая) = 360° - 130° - 110°
∪КЕ (фиолетовая) = 120°.
ответ :120°.