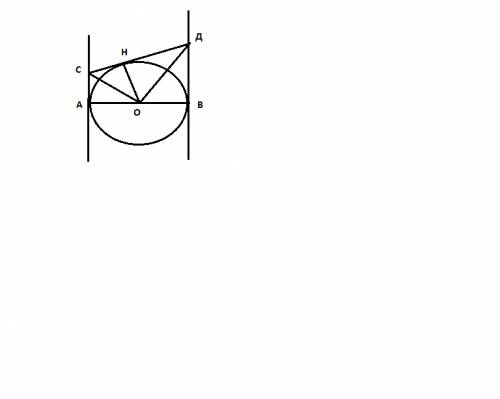
В трапеции треугольники, образованные диагоналями и боковыми сторонами, равновелики. т.е.
S ∆ АЕД=S∆ ВЕС.
Тогда S ∆ ВЕС равна полуразности между площадью трапеции и суммой площадей ∆ АВЕ и ∆ ДЕС.
∆ АВЕ~∆ ДЕС по равным вертикальным и накрестлежащим углам
k=24/30=4/5
Тогда
высота h трапеции состоит из высот этих треугольников h1 и h2; h1:h2=4/5 ⇒ h=9 частей этого отношения.
точкой Е высота трапеции делится на
h1=h*4/9
h2=h*5/9
S ∆ АВЕ=0,5*24*4h/9=12*4h/9
S ∆ ДЕС=0,5*30*5h/9=15*5h/9
Площадь трапеции
S АВСД=(24+30)*h/2=27h
Сумма площадей треугольников при основаниях
S ∆ АВЕ+S ∆ ДЕС=12*4h/9+15*5h/9=41h/3
Сумма площадей треугольников при боковых сторонах
S АВСД – (S ∆ АВЕ+S ∆ ДЕС)=27h – 41h/3=40h/3
Площадь ∆ ВСЕ равна половине полученного значения (см. выше):
S ∆ BCE=(40h/3):2=20h/3
Найдем h из ∆ АДН.
h=AH=AД*sin 60º
h=(3*√3):2=1,5√3
S ∆ BCE=20*1,5√3/3=10√3

т.к. получается что треугольник авс равнобедренный..и один угол при основании равен 15 градусов , значит и другой угол при основании равен 15 град(угол в) отсюда угол с равен 150 градусам.
т.к. угол с тупой значит перпендикуляр стороне ас будет лежать за пределами треугольника( продлить ас и построить к ней перпендикуляр из точки в)-получим точку т. и проведем отрезок кт. значит отрезок кт и будет расстоянием от точки к до прямой ас( по теореме о трех перпендикулярах)
получим треугольники ств и вкт они оба прямоугольные.
треугольник свт:
угол тсв равен 30 градусам( т.к. этот и угол асв смежные,а угол асв равен 150 градусам), по свойству отрезок против угла в 30 градусов равен половине гипотенузы,значит ст=5(гипотенуза св)
треугольник вкт:
кв= 5 корней из 3, вт =5, по теореме пифагора находим гипотенузу, кт=10
ответ:10