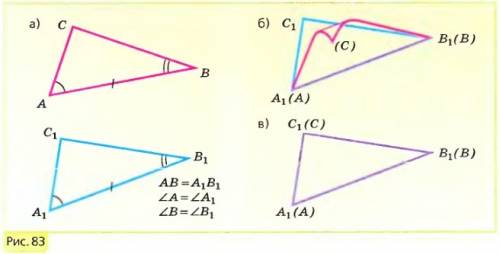
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых AB = A1B1, ∠A = ∠A1, ∠B = ∠B1 (рис. 83, а), и докажем, что эти треугольники равны.
Мысленно наложим треугольник ABC так, чтобы вершина A совместилась с вершиной A1, сторона AB – с равной ей стороной A1B1, а вершина C и C1 оказались по одну сторону от прямой A1B1 (рис. 83, б).
Так как ∠A = ∠A1 и ∠B = ∠B1, то сторона AC наложится на луч A1C1, а сторона BC – на луч B1C1. Поэтому вершина C – общая точка сторон AC и BC – совместится с общей точкой лучей A1C1 и B1C1, т. е. с точкой C1 (рис. 83, в). Из этого следует, что стороны AC и BC совместятся соответственно со сторонами A1C1 и B1C1. Итак, треугольники полностью совместятся, и, следовательно, они равны. Теорема доказана.
SM = 4 cм
Объяснение:
найдем гипотенузу основания по теореме Пифагора
АВ=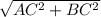 =10
=10
SO высота пирамиды, а OK,OM,ON - серединные перпендикуляры и радиусы вписанной окружности, равные между собой.
Чтобы найти радиус, воспользуемся формулой площади S=pr и
S=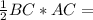 0,5*6*8=24 см^2 Тогда r=S/p, где р- полупериметр =(6+8+10)/2=12, r=24:12=2 см
0,5*6*8=24 см^2 Тогда r=S/p, где р- полупериметр =(6+8+10)/2=12, r=24:12=2 см
Треугольник SOM прямоугольный с углом 60 и 30 градусов, при вершине угол 30 градусов, катет напротив этого угла равен половине гипотенузы, значит гипотенуза (высота боковой грани) SM = 2r=4 cм