7
Теорема косинусов для треугольника AМC
AC^2=AM^2+MC^2-2*AM*CM*cosAMC
Теорема косинусов для треугольника BМC
BC^2=BM^2+MC^2-2*BM*CM*cosBMC
AC=BC (треугольник равносторонний) Тогда AC^2=BC^2
AM^2+MC^2-2*AM*CM*cosAMC=BM^2+MC^2-2*BM*CM*cosBMC
AM^2-2*AM*CM*cosAMC=BM^2-2*BM*CM*cosBMC
АМ и ВM знаем
2^2-2*2*CM*cosAMC=10^2-2*10*CM*cosBMC
4-4*CM*cosAMC=100-20*CM*cosBMC
Углы ВМС и ВАС равны, опираются на одну дугу. ВАС=60 - равносторонний треугольник.
Угол АМС=АМВ+ВМС=АСВ+ВАС=60+60=120
4-4*CM*cos120=100-20*CM*cos60
4-4*CM*(-1/2)=100-20*CM*1/2
4+2*CM=100-10*CM
12*CM=96
СМ=8
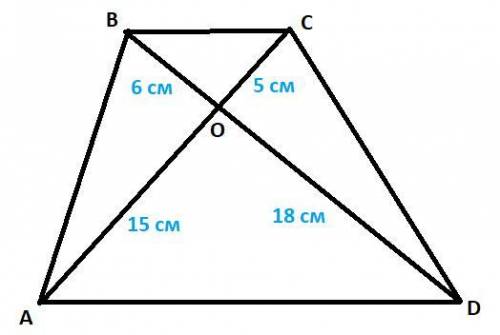
Условие: Диагонали четырехугольника ABCD AC и BD пересекаются в точке O так, что OC = 5 см, OB = 6 см, OA = 15 см, OD = 18 см. Докажите, что в четырехугольнике ABCD BC ║ AD и найдите отношение площадей треугольников AOD и BOC.
Дано: ABCD - четырехугольник, AC ∩ BD = O, OC = 5 см, OB = 6 см, OA = 15 см, OD = 18 см.
а) Доказать: BC ║ AD.
б) Найти: 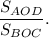
а) Доказательство:
ΔAOD подобен ΔBOC по двум пропорциональным сторонам и углу между ними:
OA/OC = 15/5 = 3/1 и OD/OB = 18/6 = 3/1 ⇒ OA/OC = OD/OB∠AOD = ∠BOC - как вертикальные углыЗначит, ∠ВСО = ∠DAO, а это равные накрест лежащие углы.
Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.
⇒ BC ║ AD, что и требовалось доказать.
б) Решение:
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
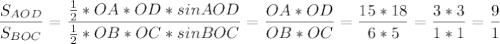
ответ: а) доказано ; б) 9 : 1.
100°
Объяснение:
Сумма углов треугольника равна 180°
третий угол=180°-(50°+30°)=180°-80°=100°
Выберите как лучший если понравится