использованы формулы: площадь полной поверхности, площадь ромба, теорема Пифагора
Площадь полной поверхности параллелепипеда равна 2 площади основания + площадь боковой поверхности. Т. к. большая диагональ парал-да образует с боковым ребром угол 45 град., то большая диагональ ромба равна боковому ребру - получается прямоугольный треугольник с острым углом 45 град. след. он равнобедренный. Находим по теореме Пифагора. Пусть ребро - х, тогда х2 + х2 = (16 корней из 2) 2, 2 х х2=16 х 2, х2=256, х=16. Вторая диагональ ромба и боковое ребро равны 16 см. Площадь ромба ноходим, как половину произведения его диагоналей, а площадь боковой поверхности - периметр основания на боковое ребро. Сторона основания (по т. Пифогора) равна корню кв. из 6 в квадрате + 8 в квадрате (диагонали ромба перпендикулярны и делятся точкой пересечения пополам) 36+64=100, т. е. 10.
S=2Sосн.+Sбок.=2 х 1/2 х 12 х16 + 10 х 4 х 16 = 16 (12+40) = 832 кв. см.
т.к треугольник равнобедренный, то высота это и медиана и биссектриса. следовательно получим два равных прямоугольных треугольника. углы в них 90 30 и 60 градусов
(углы при основании большого треугольника равны так как это равнобедренный треугольник и равны соответственно 180 - 120=60\2=30)
свойство прямоугольных треугольников, что катет лежащий против угла в 30 градусов равен половине гипотенузы
следовательно гипотенуза равна 23*2=46 см
по теореме пифагора находим основание маленького треугольника это 46^=23^2 +x^2
х= 23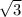
основание большого треугольника 23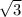
*2 = 46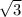
Объяснение: