В равнобедренном треугольнике ABC проведена высота BD к основанию AC. Длина высоты — 13,1 см, длина боковой стороны — 26,2 см. Определи углы этого треугольника.
Диагонали равнобедренной трапеции равны, поэтому oc: ao=ob: do=2: 5 и, так как ∢boc=∢aod, то δaod∼δboc (по второму признаку подобия треугольников: две стороны одного треугольника пропорциональны двум сторонам другого и углы, лежащие между этими сторонами равны). 2. так как δaod∼δboc, то adbc=aooc=52. из этого соотношения выражаем и вычисляем большее основание трапеции ad: ad=5×bc2=5×122=30 см. 3. вычисляем ae: ae=ad−bc2=30−122=182=9 см. 4. так как δabe — прямоугольный треугольник, то находим боковую сторону ab по теореме пифагора: ab=be2+ae2−−−−−−−−−−√=122+92−−−−−−−√=144+81−−−−−−−√=225−−−√=15 см. 5. находим периметр равнобедренной трапеции abcd: p(abcd)= 2×ab+ad+bc=2×15+30+12=72 см.
Пусть S₁ - это площадь бо́льшего треугольника, а S₂ - площадь меньшего треугольника.
Пусть k > 1 (это значит, что в числителе будет стоять бо́льший треугольник).
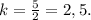
Площади подобных треугольников относятся как квадрат коэффициента подобия.Отсюда -
1,28 (ед²).
- - -
Случай 2 - Площадь меньшего треугольника равна 8 (ед²).В этом случае наоборот k < 1 (в числителе будет стоять меньший треугольник).
S₁ - площадь бо́льшего треугольника, S₂ - площадь меньшего треугольника
Тогда -
50 (ед²).