Проведем перпендикуляр SO к плоскости основания и перпендикуляры SK, SM и SN к сторонам ΔABC. Тогда по теореме о трех перпендикулярах OK ⊥ BC, ОМ ⊥ АС и ON ⊥ AB.
Тогда, ∠SKO = ∠SMO = ∠SNO = 45° — как линейные углы данных двугранных углов.
А следовательно, прямоугольные треугольники SKO, SMO и SNO равны по катету и острому углу.
Так что OK=OM=ON, то есть точка О является центром окружности, вписанной в ΔАВС.
Выразим площадь прямоугольника АВС:
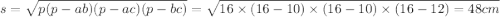
С другой стороны можно S=p×r
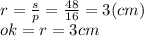
Так как в прямоугольном треугольнике SOK острый угол равен 45°, то ΔSOK является равнобедренным и SO=OK=3 см.
ответ: 3 см.
Пусть сторона куба равна x, тогда диагональ основания равна sqrt(x^2+x^2)=x*sqrt(2), а диагональ куба равна sqrt(2x^2+x^2)=sqrt(3x^2)=x*sqrt(3)
С другой стороны
x*sqrt(3)=11
то есть x=11/sqrt(3), а поверхность куба равна 6*11/sqrt(3)=sqrt(1452)