Question

Найдите координаты центра окружности и ее радиус, если известно уравнение окружности а)(x+2)^2+y^2=9; б)x^2+(y-4)^2=8; в) (x-5)^2+(y+7)^2=16

Answer 1

а) (-2;0) - центр окружности, радиус окружности равен 3.

б) (0; 4) - центр окружности, радиус окружности равен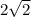 $2\sqrt{2}$.

в) (5; -7) - центр окружности, радиус окружности равен 4.

Объяснение:

Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.

а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.

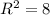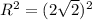
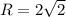б) (0; 4) - центр окружности, $R^2=8$, $R^2=(2\sqrt{2})^2$  $R=2\sqrt{2}$.

в) (5; -7) - центр окружности, R²=16,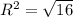 $R^2=\sqrt{16}$,  R=4.

Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень