Прямые ОА и АС - являются секущими по отношению к данной окружности.
Объяснение:
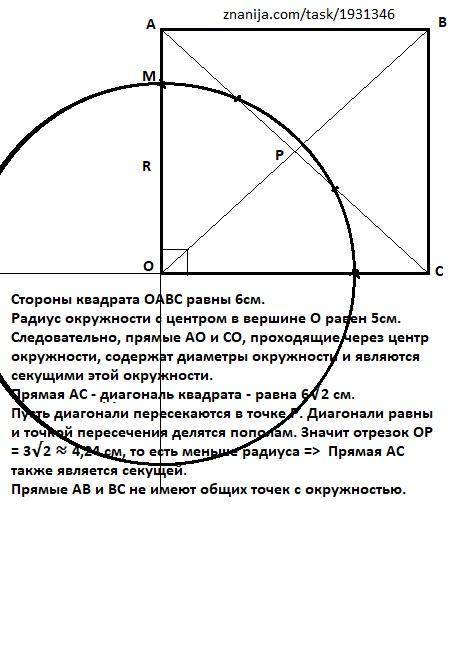
Стороны квадрата ОАВС равны 6см.
Радиус окружности с центром в вершине О равен 5см.
Следовательно, прямые АО и СО, проходящие через центр окружности, содержат диаметры окружности и являются секущими этой окружности.
Прямая АС - диагональ квадрата - равна 6√2 см.
Пусть диагонали пересекаются в точке Р. Диагонали равны и точкой пересечения делятся пополам. Значит отрезок ОР = 3√2 ≈ 4,24 см, то есть меньше радиуса => Прямая АС также является секущей.
Прямые АВ и ВС не имеют общих точек с окружностью.
1) у= Ох+р
2) х= Оу+q
3) ах+bу+с=0
4) у-у1/у2-у1=х-х1/х2-х1
удачи)