Точка А принадлежит прямой AD. Прямая AD параллельна ВС, следовательно, параллельна плоскости BSC, поэтому все её точки находятся на одинаковом расстоянии от этой плоскости.
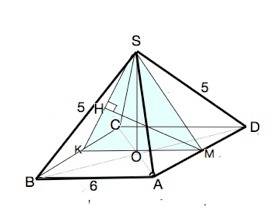
Проведем в противоположных гранях пирамиды сечение через апофемы SK и SM.
М - основание апофеы на AD, AM=DM=3.
SM=SK=4 ( ∆ ASM - египетский.
В ∆ SOK по т.Пифагора SO=√(SK²-OK²)=√(16-9)=√7
sin∠SKO=SO:SK=√7/4
Искомое расстояние от точки М до плоскости - длина отрезка МН, проведенного к ней перпендикулярно, оно равно расстоянию от А до той же плоскости (см. выше).
МН=КМ•sin∠SKO=6•√7/4=3√7/2
1)Рассмотрим треугольник ACD, тк по условию CD=3.5=1/2*7, то угол А=30(катет, лежащий против угла в 30 градусов = половине гипотенузы), следовательно угол D=180-(90+30)=60 градусов.
2)Рассмотрим треугольник ABD, он равнобедренный по условию(AB=AD), значит угол D = углу B = 60.
Объяснение: