Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство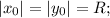
учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти) 
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
;
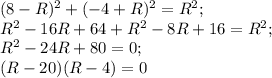R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
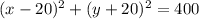
и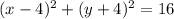 
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
k_1k_2=-1
поєтому угловой коєффициент искомой пряммой равен k=-1/(-0.5)=2
учитывая что искомая пряммая проходит через точку С ищем ее уравнение в виде
y=kx+b (k=2)
2=2*0+b;
b=2
y=2x+2 или y-2x-2=0
в чем ошибка у вас - неведомо, ибо вы своего решения не предоставили
Вся трудность заключается в нахождении большего основания.
Оно равно сумме меньшего основания и двух катетов прямоугольных треугольников, образованных боковой стороной и высотой трапеции (треугольники равны между собой по гипотенузе и катету, а значит и требуемые катеты тоже равны).
Найдем катет.
По теореме Пифагора:
4^2 + x^2 = 5^2.
16 + х^2 = 25.
x^2 = 9
x = 3.
Следовательно, требуемый катет = 3 см. Таких треугольников два, как уже говорилось.
Большая сторона трапеции = 6 + 3 + 3 = 12 см.
Теперь найдем площадь трапеции: полусумма оснований на высоту.
(6+12)/2 * 4 = 36 см^2
могу только на 1 и 3
1.По свойствуву угла в 30° в прямоугольном треугольнике
АВ=2*ВС
ВС=15/2=7.5
ответ:ВС=7.5
3.т.к АС=6 см и АD=DC,тогда AD=3 cм
в треугольнике АВС угол ВАD =45 градусов и угол BDA=90 градусов значит угол ABD=45 градусов (по сумме углов в треугольнике).
треугольник BAD равнобедренный и AD=BD=3cм.