BD1
Объяснение:
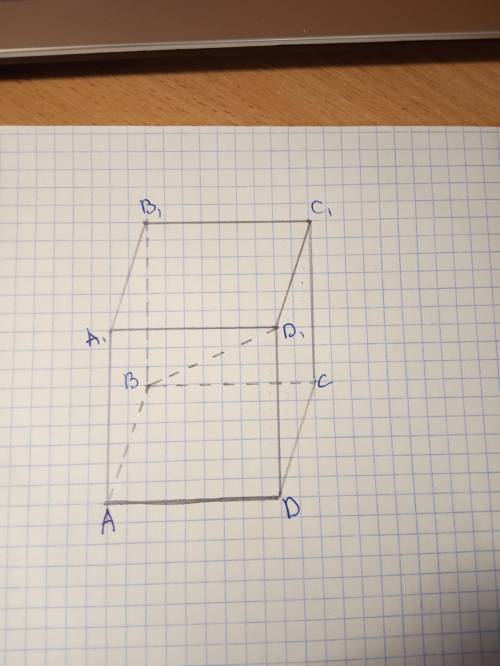
Фигура ACB1B - правильная треугольная пирамида. В основании её равносторонний треугольник ACB1: AC = AB1 = CB1 (диагонали граней куба), и боковые ребра равны между собой BA = BC = BB1; (это просто стороны куба). Это означает, что точка B проектируется на плоскость ACB1 в центр треугольника ACB1 - точку O. (ну, у равностороннего треугольника все центры совпадают, можете выбирать, какой именно центр, но по логике это центр описанной окружности). То есть, BO перпендикулярно плоскости ACB1.
Фигура ACB1D1 - тоже правильная треугольная пирамида, причем у неё равны между собой все ребра (все ребра этой пирамиды - диагонали граней куба). Поэтому D1O перпендикулярно плоскости ACB1;.
Поскольку через точку O можно провести только один перпендикуляр к плоскости ACB1, точки B, O, D1 лежат на одной прямой, перпендикулярной плоскости ACB1, то есть прямая D1B и есть тот самый перпендикуляр на плоскость ACB1.
PS: Извиняйте за кривой рисунок, линейки при себе не было, всё делалось на скорую руку
1) Окружность называется вписанной в треугольник, если она касается всех его сторон. Окружность называется описанной около треугольника, если она проходит через все его вершины. Теорема 1. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
2) Центром является точка (принято обозначать О) пересечения серединных перпендикуляров к сторонам многоугольника.
3) Если прямоугольный треугольник вписан в окружность, значит его гипотенуза - диаметр. Следовательно по теореме Пифагора:
2R = корень из (36+64) и тогда R = 5 (см).
4) Свойство четырехугольника. Четырехугольник можно описать вокруг тогда и только тогда, когда суммы длин его противоположных сторон равны
Пусть по условию a+c=15. Тогда a+c=b+d; 15=b+d
Периметр четырехугольника: P=a+b+c+d=(a+c)+(b+d)=15+15=30 см
5) прости не смог
Объяснение: