0,2
Объяснение:
ΔOAB - прямоугольный, <BOA = 45°, ⇒ <ABO = 90° - 45° = 45°, ⇒ ΔOAB - равнобедренный, ⇒ OA = OB.
Пусть AB = x, тогда AD = x = CD, т.к. ABCD - квадрат.
Построим отрезок OC, OC - радиус по построению, т.к. О - центр окружности, а точка C лежит на окружности, ⇒ OC = 1.
Рассмотрим прямоугольный ΔODC: OD = OA + AD = x + x = 2x, CD = x, тогда по теореме Пифагора OC² = OD² + CD² , получаем уравнение:
1² = (2x)² + x²
1 = 4x² + x²
5x² = 1
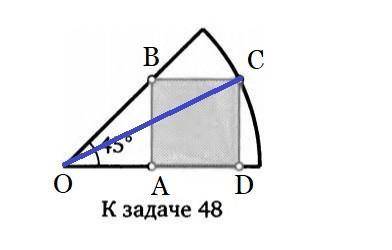
x² = 1/5 = 0,2
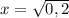 - сторона квадрата, тогда площадь квадрата x² = 0,2
- сторона квадрата, тогда площадь квадрата x² = 0,2
Нет
Объяснение:
Сумма углов выпуклого многоугольника находится по формуле S = (n-2)*180°, где n - количество углов или сторон многоугольника.
Найдем по формуле сумму углов выпуклого семиугольника: S = (7 - 2)*180° = 5*180° = 900°.
Допустим, что наименьший угол 136°. Допустим, что все остальные углы равны, тогда они больше 136° на величину x°.
Тогда получим: 136° + 6*(136° + x°) = 900°
136° + 816° + 6x° = 900°
6x° = 900° - 952°
6x° = -52°
x =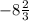 °, т.е. получаем противоречие, т.к. x - отрицательно, т.е остальные углы в таком случае меньше 136°, а значит 136° не наименьший угол.
°, т.е. получаем противоречие, т.к. x - отрицательно, т.е остальные углы в таком случае меньше 136°, а значит 136° не наименьший угол.
ответ: нет