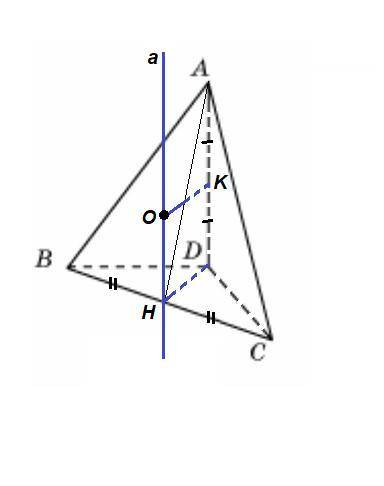
1) Через середину гипотенузы строим прямую а, перпендикулярную основанию.
2) В плоскости, которая задается этой прямой и ребром AD проводим серединный перпендикуляр к AD.
3) Точка пересечения серединного перпендикуляра и прямой а - центр описанной сферы.
Объяснение:
Если сфера описана около данной пирамиды, то основание пирамиды вписано в окружность - сечение сферы.
Основание - прямоугольный треугольник. Центр описанной около него окружности лежит на середине гипотенузы.
Пусть Н - середина гипотенузы ВС прямоугольного треугольника BCD.
Тогда точка Н - центр окружности, описанной около ΔBCD, равноудалена от всех вершин основания.
Отрезок, соединяющий центр сечения сферы с центром сферы, перпендикулярен сечению.Проведем через точку Н прямую а║AD. AD⊥(BCD), так как AD⊥BD и AD⊥DC, значит а⊥(BCD).
Центр сферы будет лежать на прямой а.
Любая точка прямой а равноудалена от вершин основания. Осталось найти на ней точку, удаленную от вершины А на то же расстояние, что и от остальных вершин.
Для этого в плоскости (ADH) проведем серединный перпендикуляр к ребру AD. К - середина AD, проведем КО║DН до пересечения с прямой а.
О - центр сферы.
Подставим координаты точек А и В в уравнение эллипса с учётом того, что он симметричный относительно осей координат.
(200/9а²) + (4/9в²) = 1,
(50/4а²) + (1/в²) = 1.
Приводим к общему знаменателю.
200в² + 4а² = 9а²в².
50в² + 4а² = 4а²в².
Умножим обе части первого уравнения на 4, а второго на 9.
800в² + 16а² = 36а²в².
450в² +36а² = 36а²в².
Вычтем из первого второе.
350в² + 20а² = 0.
Отсюда получаем а² = (35/2)в² и подставим во второе уравнение.5
50в² + 70в² = 70в⁴.
Получаем биквадратное уравнение 70в⁴ - 120в² = 0.
Сократим на 10 и сделаем замену в² = t.
7t² - 12t = 0,
t(7t - 12) = 0. t1 = 0, t2 = 12/7.
Отсюда находим значение полуосей:
в1 = 0 (не принимаем) и в2 = +-√(12/7) =+-2√(3/7).
а = +-√((35/7)*(12/7)) = +-√30.
ответ: |а| = √30, |b| = 2√(3/7).