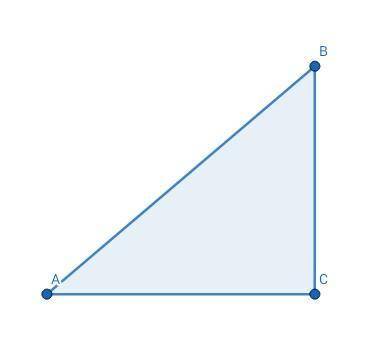
1 случай, где катет ВС = 4,2 см
Если катет равен половине гипотенузы, то напротив лежащий угол равен 30°.
=> ∠А = 30°.
Сумма острых углов прямоугольного треугольника равна 90°.
∠В = 90° - 30° = 60°
ответ: 60°, 30°.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
2 случай, где АС = 4,2 см.
Если катет равен половине гипотенузы, то напротив лежащий угол равен 30°.
=> ∠В = 30°
Сумма острых углов прямоугольного треугольника равна 90°.
∠А = 90° - 30° = 60°
ответ: 30°, 60°.
Решение: точка О - центр вписанной окружности радиусом r
Точка F - основание высоты равнобедренного треугольника на стороне ac
из точки Е на стороне ab - высоту треугольника abO. ее длинна равна r
Треугольники abF и ebO - подобны по двум углам.
Пропорция Fb/ab = eb/Ob
Fb=Ob+FO=15+r
ab=30
eb =
Ob = 15
(15+r)/30 =
После приведения
225+30r+
Решение квадратного уравнения - два ответа: 9 и -15
r = 9
Зная радиус находим длину биссектрисы Fb = 15+9 =24
В треуг. abF по теореме Пифагора сторона af = 18
P = 30+30+18*2 = 96
Возможны неточности в математических определениях - лет 15 в математику не лез. Удачи.