Получилось как-то многословно, но, надеюсь, понятно)
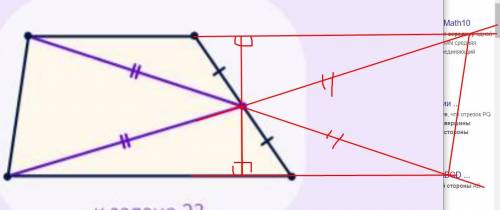
Продолжим прямые, соединяющие середину боковой стороны с двумя вершинами, до пересечения с продолжениями сторон.
Из равенства прямоугольных треугольников (прямой угол, равное расстояние от оснований трапеции и вертикальный угол) будет следовать тот факт, что точка пересечения диагоналей новой фигуры делит эти диагонали пополам.
Следовательно, мы построили параллелограмм (это его свойство). По рисунку так же понятно, что диагонали нашего параллелограмма будут равны друг другу. Но из всех видов параллелограмма лишь у прямоугольника диагонали могут быть равны друг другу, следовательно, на самом деле мы построили прямоугольник. Ну а раз у нашей новой фигуры все углы прямые, то и у трапеции 2 левых угла равны 90°, что и говорит о её прямоугольности.
1. ∠ABD = ∠AMK как соответственные при пересечении параллельных прямых BD и МК,
∠А - общий для треугольников ABD и AMK, значит
Δ ABD подобен ΔAMK по двум углам.
AB : AM = BD : MK
AB : 32 = 4 : 8
AB = 32 · 4 / 8 = 16 см
2. ∠ОАВ = ∠ОМК как накрест лежащие при пересечении параллельных прямых АВ и МК,
∠О - общий для треугольников АОВ и МОК, значит
ΔАОВ подобен ΔМОК по двум углам.
АB : MK = AO : MO
AB : 10 = 8 : 20
AB = 10 · 8 / 20 = 4
3. AD : AB = 6 : 15 = 2 : 5
AK : AC = 8 : 20 = 2 : 5
∠A - общий для треугольников ADK и АВС, значит
ΔADK подобен ΔABC по двум пропорциональным сторонам и углу между ними.
DK : BC = AD : AB = 2 : 5
DK : 30 = 2 : 5
DK = 30 · 2 / 5 = 12 см
4. Площади подобных треугольников относятся, как квадрат коэффициента подобия:
k² = S₁ : S₂ = 64/81
k = √(64/81) = 8/9
a₁ : a₂ = 8 : 9
Из условия задачи не ясно, какому из треугольников принадлежит сторона, равная 8. Рассмотрим два случая:
1) a₁ = 8
8 : a₂ = 8 : 9
a₂ = 8 · 9 / 8 = 9
2) a₂ = 8
a₁ : 8 = 8 : 9
a₁ = 8 · 8 / 9 = 64/9 = 7_1/9