Диаметр = 2 радиусам.
следовательно 20 дм умножить на 2 = 40 дм ну или 400 см
Объяснение:
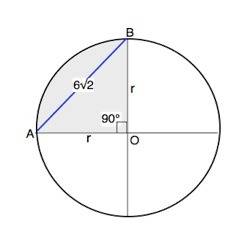
Обозначим хорду АВ, центр окружности - О.
Центральный угол АОВ опирается на хорду, стягивающую дугу 90°, ⇒ ∠АОВ=90°.
∆ АОВ- прямоугольный равнобедренный ( катеты - радиусы окружности). Его острые углы равны 45°
r=АО=ВО=АВ•sin45°=6√2•√2:2=6
С - длина окружности.
С=2π•r=12π
Дуга 90°=90°:360°=1/4
L=12π:4=3π -( четверть длины окружности).
Площадь сектора с углом 90°=1/4 площади круга.
S=πr²=36π
S сект=36π/4=9π
-------
Сектор с углом 90° - частный случай. Формула площади сектора через угол сектора круга:
S=πr²α/360º, где α - угол сектора круга.
Видимо надо найти стороны ПРЯМОУГОЛЬНИКА! Так как стороны ТРЕУГОЛЬНИКА в условии даны!
Рисунок смотри во вложении.
Пусть х и у - стороны пр-ка. Проведем дополнительно высоту ВЕ тр-ка АВС.
Найдем ее. Площадь по формуле Герона:
S = корень(48*28*14*6) = 336 (полупериметр р = 48)
С другой стороны:
S = (1/2)*42*BE = 336
Отсюда ВЕ = 16
Из подобия тр-ов ВКМ и АВС:
х/42 = ВК/20
Отсюда ВК = 10х/21, АК = 20 -10х/21 = (420-10х)/21
Из подобия тр-ов АКР и АВЕ:
у/16 = АК/20
Или: у/16 = (42-х)/42
8х + 21у = 336
Другое уравнение системы получим из условия, что периметр пр-ка равен 40:
х + у = 20. Домножим это уравнение на (-8) и сложим с предыдущим.
13у = 176
у = 176/13, тогда х = 20 - 176/13 = 84/13
ответ: 176/13; 84/13.
Объяснение: диаметр = 2 радиусам. то есть 20 дм * на 2 = 40 дм или 400 см