Очень На гипотенузе АВ прямоугольного треугольника АВС взята точка Е, а внутри треугольника - точка К. Перпендикуляр ЕМ к прямой АС делит катет АС пополам. ∠ В =45", ∠С=90" , ∠СКА = 90" , ∠КСА= 60". Доказать, что ЕМ=СК.
1.) Стороны данного острого угла параллельны плоскости α. Докажите, что и биссектриса параллельна этой плоскости.
2. Прямые a i b которые пересекаются, пересекают три данные параллельные плоскости α, β, γ в точках А₁,А₂,А₃ и В₁,В₂,В₃ соответственно. Найти B₁B₃ ,если А₁А₂=25см, В₂В₃=4 см,А₂А₃+В₁В₂=20 см (на фото рисунок к задачи).
Объяснение:
1)Стороны острого угла определяют плоскость β единственным образом как и пересекающиеся прямые.И эта плоскость β║α ⇒ все прямые плоскости β параллельны α и значит биссектриса угла параллельна α.
2)Пересекающиеся прямы а и в определяют плоскость , которая пересекает плоскости α, β, γ , единственным образом. Линии пересечения плоскостей будут параллельны , т.е. А₁В₁║А₂В₂║А₃В₃ . Введем для простоты записей обозначения А₂А₃=х , В₁В₂=у , тогда х+у=20.
По т. о пропорциональных отрезках , но х=20-у ⇒
, y²-20y+100=0 ,(y-10)²=0 ,y=10
B₁B₃ =B₁B₂+В₂В₃=10+4=14 (cм)
==============================
Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.
Найлем для начало стороны AB=√(8-4)^2+(2-6)^2 =√ 16 +16=2√8CD=√(-2-4)^2+(-1+3)^2 =√36+4 =√40 BC=√(4-8)^2+(-3-2)^2=√16+25=√41AD=√(-2-4)^2+(-1-6)^2=√36+49=√85 на рисунке можно видеть что это трапеция выходит, можно раздлить эту трапецию на два треугольника затем найти площадь каждой и суммировать Площадь треугольника S=ab/2*sinaнайдем угол между АВ и AD через скалярAB {4;-4}AD{-6;-7}cosa=4*-6+ 4*7 / √32*85 = 4/√2720теперь sina=√1-16/2720=52/√2720теперь площадь S= 52/√2720 * √2720/2 = 26 теперь площадь другого треугольника опять угол B (8; 2), C (4; -3), D (-2; -1) ВС={-4;-5} CD={-6;2} cosa= 24-10/√1640 = 10/√1640 sina = √1-100/1640 = √1540/1640 S=√41*40/2 * √1540/1640 =√1540/2 = √385 S=√385+26 площадь искомая
1.) Стороны данного острого угла параллельны плоскости α. Докажите, что и биссектриса параллельна этой плоскости.
2. Прямые a i b которые пересекаются, пересекают три данные параллельные плоскости α, β, γ в точках А₁,А₂,А₃ и В₁,В₂,В₃ соответственно. Найти B₁B₃ ,если А₁А₂=25см, В₂В₃=4 см,А₂А₃+В₁В₂=20 см (на фото рисунок к задачи).
Объяснение:
1)Стороны острого угла определяют плоскость β единственным образом как и пересекающиеся прямые.И эта плоскость β║α ⇒ все прямые плоскости β параллельны α и значит биссектриса угла параллельна α.
2)Пересекающиеся прямы а и в определяют плоскость , которая пересекает плоскости α, β, γ , единственным образом. Линии пересечения плоскостей будут параллельны , т.е. А₁В₁║А₂В₂║А₃В₃ . Введем для простоты записей обозначения А₂А₃=х , В₁В₂=у , тогда х+у=20.
По т. о пропорциональных отрезках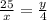 , но х=20-у ⇒
, но х=20-у ⇒ 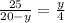
, y²-20y+100=0 ,(y-10)²=0 ,y=10
B₁B₃ =B₁B₂+В₂В₃=10+4=14 (cм)
==============================
Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.