При пересечении двух прямых появляются вертикальные углы.
Одно из свойств вертикальных углов - противоположные углы при их создании равны
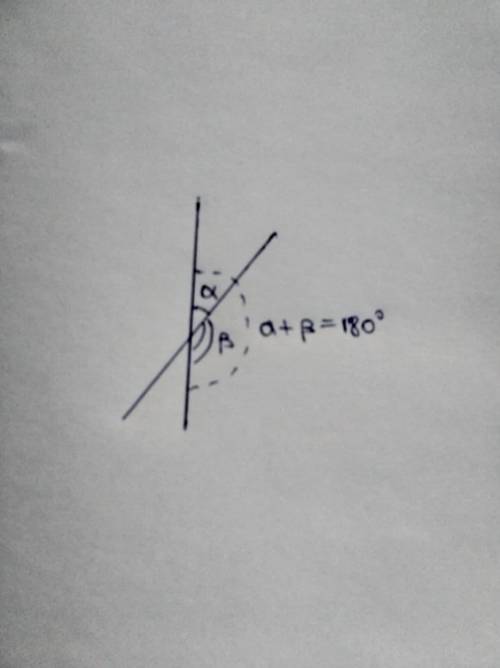
Рассмотрим пример: на фото ниже мы видим вертикальные углы на практике. При создании вертикальных углов пара малого и большего угла создают развёрнутый угол в 180°.
Как мы видим, при разности углов данной пары противоположные углы равны, отсюда - равенство лишь двух углов
Рассмотрим наши требования. Если провести перпендикуляр с какой-либо точки, увидим следующее: перпендикуляр создаёт угол в 90°. Соседний прямой угол прямого угла создают в сумме 180°. Продолжая перпендикуляр по идентичной траектории, увидим, что на обратной стороне прямой будут такие же прямые углы. Следуя по таким соображениям, мы можем заметить, что все углы равны и наши условия пересечения двух прямых полностью справедливы и действительны
Что и требовалось доказать
Мне казалось я уже выкладывал решение, но почему-то не могу найти, наверно был особо принципиален в тот момент. Но чертеж сохранился, на нем решение легко просматривается.
На самом деле это всего лишь упражнение на общие свойства инверсии, главное из которых - конформность (то есть сохранение углов). См. чертеж.
Ясно, что прямые OA, OC и OB перейдут в себя, и образы A' B' C' будут лежать на этих прямых (соответственно). При этом прямые AB и BC перейдут в окружности, проходящие через точку O. На чертеже изображены эти окружности OA'B' и OC'B'. При этом углы между касательными к этим окружностям и прямыми-образами (которые совпадают с исходными) сохраняются. То есть если провести касательную в точке B' к окружности OA'B' то угол между ней и прямой OB будет 20° (такой же, как ∠OBA).
=> эта касательная параллельна OA, => дуги OB' и B'A' равны,
=> ∠B'A'O = 20°.
∠OA'C' = ∠OAC = 90° - 20° = 70°
Дальше сосчитать, чему равен ∠B'A'C', совсем просто.
∠B'A'C' = ∠OA'C' - ∠B'A'O = 50°

талыми снегами и ледниками