Дано:
Прямоугольный треугольник.
Угол С=90°, А=60°, В=30°
Сторона АС=4
Найти: Сторону АВ
АС катет, который лежит на против угла В=30°
А мы знаем теорему:
Напротив угла в 30 градусов лежит катет равный половине гипотенузы.
Получается, чтобы найти сторону АВ, нам нужно:
4*2=8
АВ=8см
ответ: 8см
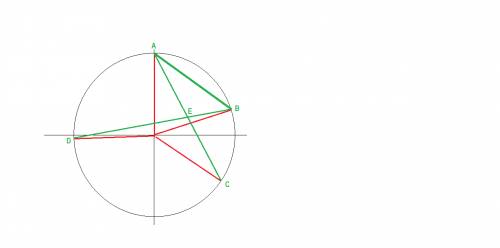
сделаем построение по условию
соединим точки А и В
найдем углы треугольника АЕВ
<ABD -вписаный - опирается на дугу (AD)
его величина РАВНА половине размера дуги
<ABD=<ABE=92/2=46
<ВАС -вписаный - опирается на дугу (ВС)
его величина РАВНА половине размера дуги
<ВАС=<BAE=48/2=24
два угла нашли
сумма углов в треугольнике 180 град
<AEB =180 -<ABE -<BAE =180-46-24=110 град
угол <AEC =180 - развернутый
<BEC и <AEB -смежные
<BEC =180-<AEB =180-110=70 град
ОТВЕТ <АЕВ=110 ; <ВЕС=70
1)Т.к. треугольник АВС-прямоугольный, то по свойству прямоугольного треугольника(катет,лежащий против угла в 30° равен половине гипотенузы)