90°, 60°, 30°, 14 см., 7 см
Объяснение:
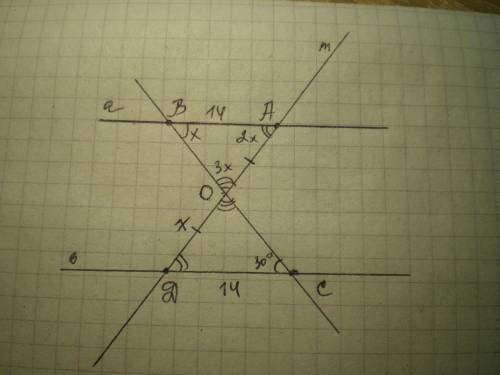
Рассмотрим ΔВАО. Пусть ∠ОВА=х°, ∠ВАО=2х°, ∠ВОА=3х°, тогда
х+2х+3х=180, т.к.сумма углов треугольника составляет 180°
6х=180; х=30.
∠ОВА=30°, ∠ВАО=2*30=60°, ∠ВОА=3*30=90°
Рассмотрим ΔСОD. ∠СОD=∠ВОА=90° как вертикальные
∠ОDС=∠ВАО=60° как внутренние накрест лежащие при а║в и секущей m
∠ОСD=∠АВО=30° как внутренние накрест лежащие при а║в и секущей m
ΔАВО=ΔСОD по стороне и двум прилежащим к ней углам, т.к. DO=АО по условию, значит СD=АВ=14 см.
ΔCOD - прямоугольный, ∠COD=90°, ∠OСD=30°, значит, OD=1/2 CD=7 см (по свойству катета, лежащего против угла 30°)
1. /АВС - вписанный(60°)
2. /АОС - центральный(80°)
3. /АВС - вписанный(90°)
4. /АDС - вписанный(160°)
5. /АВС - вписанный(125°)
6. /АОВ - центральный(160°)
7. /ADC - вписанный(30°)
8. /АВD - вписанный(90°), /СВD - вписанный(120°)
9. /DAC - вписанный(55°)
Объяснение:
Центральный угол равен дуге, на которую он опирается.
Вписанный угол равен половине дуги, на которую он опирается.
Вертикальные углы равны.
Сумма углов треугольника - 180°.
Градусная мера окружности - 360°.
Вписанный угол в 2 раза меньше центрального угла.